Deep Upper Confidence Bound Algorithm for Contextual Bandit Ranking of Information Selection
Paper and Code
Oct 08, 2021
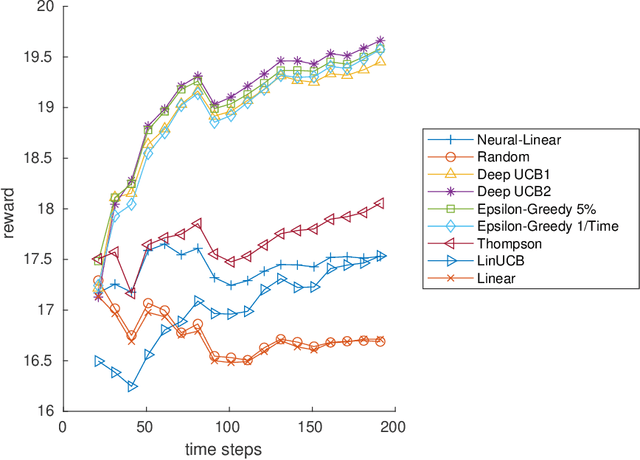
Contextual multi-armed bandits (CMAB) have been widely used for learning to filter and prioritize information according to a user's interest. In this work, we analyze top-K ranking under the CMAB framework where the top-K arms are chosen iteratively to maximize a reward. The context, which represents a set of observable factors related to the user, is used to increase prediction accuracy compared to a standard multi-armed bandit. Contextual bandit methods have mostly been studied under strict linearity assumptions, but we drop that assumption and learn non-linear stochastic reward functions with deep neural networks. We introduce a novel algorithm called the Deep Upper Confidence Bound (UCB) algorithm. Deep UCB balances exploration and exploitation with a separate neural network to model the learning convergence. We compare the performance of many bandit algorithms varying K over real-world data sets with high-dimensional data and non-linear reward functions. Empirical results show that the performance of Deep UCB often outperforms though it is sensitive to the problem and reward setup. Additionally, we prove theoretical regret bounds on Deep UCB giving convergence to optimality for the weak class of CMAB problems.
 Add to Chrome
Add to Chrome Add to Firefox
Add to Firefox Add to Edge
Add to Edge