Range-Restricted Interpolation through Clausal Tableaux

We show how variations of range-restriction and also the Horn property can be passed from inputs to outputs of Craig interpolation in first-order logic. The proof system is clausal tableaux, which stems from first-order ATP. Our results are induced by a restriction of the clausal tableau structure, which can be achieved in general by a proof transformation, also if the source proof is by resolution/paramodulation. Primarily addressed applications are query synthesis and reformulation with interpolation. Our methodical approach combines operations on proof structures with the immediate perspective of feasible implementation through incorporating highly optimized first-order provers.

Lemmas: Generation, Selection, Application

Noting that lemmas are a key feature of mathematics, we engage in an investigation of the role of lemmas in automated theorem proving. The paper describes experiments with a combined system involving learning technology that generates useful lemmas for automated theorem provers, demonstrating improvement for several representative systems and solving a hard problem not solved by any system for twenty years. By focusing on condensed detachment problems we simplify the setting considerably, allowing us to get at the essence of lemmas and their role in proof search.

Generating Compressed Combinatory Proof Structures -- An Approach to Automated First-Order Theorem Proving

Representing a proof tree by a combinator term that reduces to the tree lets subtle forms of duplication within the tree materialize as duplicated subterms of the combinator term. In a DAG representation of the combinator term these straightforwardly factor into shared subgraphs. To search for proofs, combinator terms can be enumerated, like clausal tableaux, interwoven with unification of formulas that are associated with nodes of the enumerated structures. To restrict the search space, the enumeration can be based on proof schemas defined as parameterized combinator terms. We introduce here this "combinator term as proof structure" approach to automated first-order proving, present an implementation and first experimental results. The approach builds on a term view of proof structures rooted in condensed detachment and the connection method. It realizes features known from the connection structure calculus, which has not been implemented so far.

CD Tools -- Condensed Detachment and Structure Generating Theorem Proving (System Description)

CD Tools is a Prolog library for experimenting with condensed detachment in first-order ATP, which puts a recent formal view centered around proof structures into practice. From the viewpoint of first-order ATP, condensed detachment offers a setting that is relatively simple but with essential features and serious applications, making it attractive as a basis for developing and evaluating novel techniques. CD Tools includes specialized provers based on the enumeration of proof structures. We focus here on one of these, SGCD, which permits to blend goal- and axiom-driven proof search in particularly flexible ways. In purely goal-driven configurations it acts similarly to a prover of the clausal tableaux or connection method family. In blended configurations its performance is much stronger, close to state-of-the-art provers, while emitting relatively short proofs. Experiments show characteristics and application possibilities of the structure generating approach realized by that prover. For a historic problem often studied in ATP it produced a new proof that is much shorter than any known one.

Applying Second-Order Quantifier Elimination in Inspecting Gödel's Ontological Proof

In recent years, G\"odel's ontological proof and variations of it were formalized and analyzed with automated tools in various ways. We supplement these analyses with a modeling in an automated environment based on first-order logic extended by predicate quantification. Formula macros are used to structure complex formulas and tasks. The analysis is presented as a generated type-set document where informal explanations are interspersed with pretty-printed formulas and outputs of reasoners for first-order theorem proving and second-order quantifier elimination. Previously unnoticed or obscured aspects and details of G\"odel's proof become apparent. Practical application possibilities of second-order quantifier elimination are shown and the encountered elimination tasks may serve as benchmarks.

Learning from Łukasiewicz and Meredith: Investigations into Proof Structures (Extended Version)

The material presented in this paper contributes to establishing a basis deemed essential for substantial progress in Automated Deduction. It identifies and studies global features in selected problems and their proofs which offer the potential of guiding proof search in a more direct way. The studied problems are of the wide-spread form of "axiom(s) and rule(s) imply goal(s)". The features include the well-known concept of lemmas. For their elaboration both human and automated proofs of selected theorems are taken into a close comparative consideration. The study at the same time accounts for a coherent and comprehensive formal reconstruction of historical work by {\L}ukasiewicz, Meredith and others. First experiments resulting from the study indicate novel ways of lemma generation to supplement automated first-order provers of various families, strengthening in particular their ability to find short proofs.

Facets of the PIE Environment for Proving, Interpolating and Eliminating on the Basis of First-Order Logic

PIE is a Prolog-embedded environment for automated reasoning on the basis of first-order logic. Its main focus is on formulas, as constituents of complex formalizations that are structured through formula macros, and as outputs of reasoning tasks such as second-order quantifier elimination and Craig interpolation. It supports a workflow based on documents that intersperse macro definitions, invocations of reasoners, and LaTeX-formatted natural language text. Starting from various examples, the paper discusses features and application possibilities of PIE along with current limitations and issues for future research.

KBSET -- Knowledge-Based Support for Scholarly Editing and Text Processing with Declarative LaTeX Markup and a Core Written in SWI-Prolog

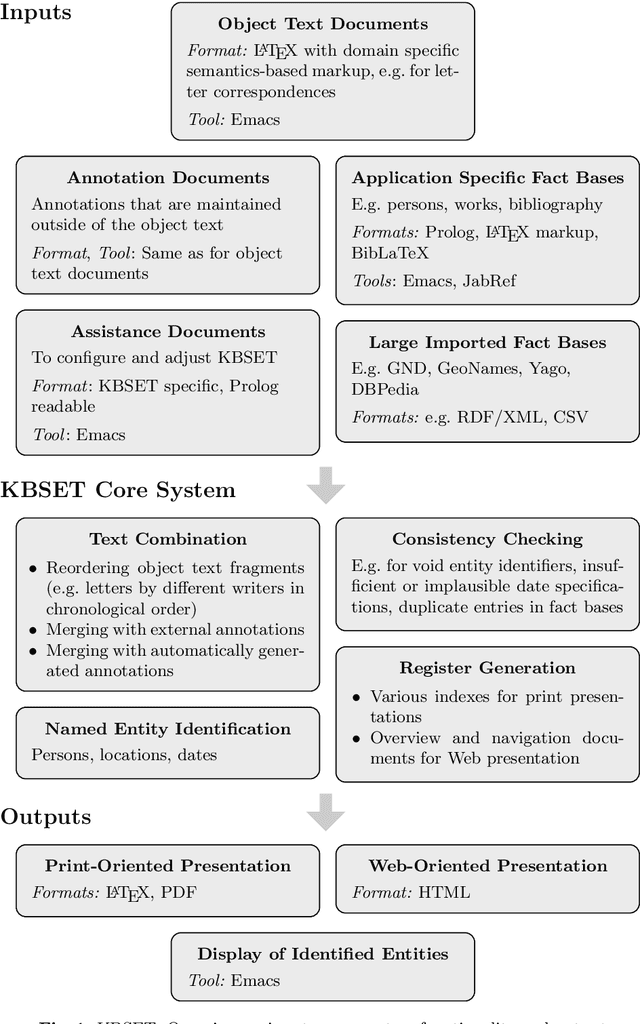
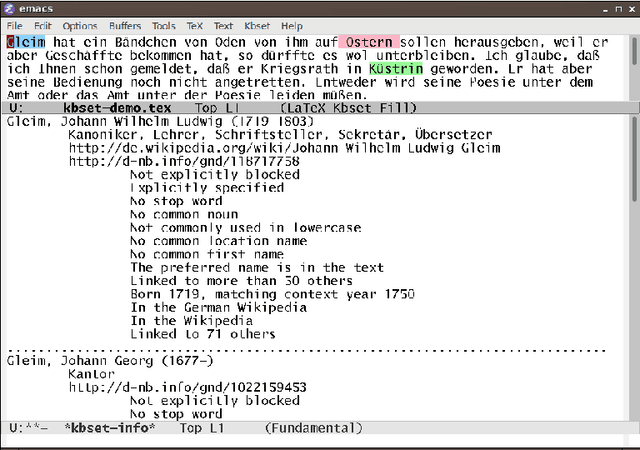
KBSET is an environment that provides support for scholarly editing in two flavors: First, as a practical tool KBSET/Letters that accompanies the development of editions of correspondences (in particular from the 18th and 19th century), completely from source documents to PDF and HTML presentations. Second, as a prototypical tool KBSET/NER for experimentally investigating novel forms of working on editions that are centered around automated named entity recognition. KBSET can process declarative application-specific markup that is expressed in LaTeX notation and incorporate large external fact bases that are typically provided in RDF. KBSET includes specially developed LaTeX styles and a core system that is written in SWI-Prolog, which is used there in many roles, utilizing that it realizes the potential of Prolog as a unifying language.

PIE -- Proving, Interpolating and Eliminating on the Basis of First-Order Logic

PIE is a Prolog-embedded environment for automated reasoning on the basis of first-order logic. It includes a versatile formula macro system and supports the creation of documents that intersperse macro definitions, reasoner invocations and LaTeX-formatted natural language text. Invocation of various reasoners is supported: External provers as well as sub-systems of PIE, which include preprocessors, a Prolog-based first-order prover, methods for Craig interpolation and methods for second-order quantifier elimination.

KBSET -- Knowledge-Based Support for Scholarly Editing and Text Processing

KBSET supports a practical workflow for scholarly editing, based on using LaTeX with dedicated commands for semantics-oriented markup and a Prolog-implemented core system. Prolog plays there various roles: as query language and access mechanism for large Semantic Web fact bases, as data representation of structured documents and as a workflow model for advanced application tasks. The core system includes a LaTeX parser and a facility for the identification of named entities. We also sketch future perspectives of this approach to scholarly editing based on techniques of computational logic.