Compositional Generalization with Grounded Language Models

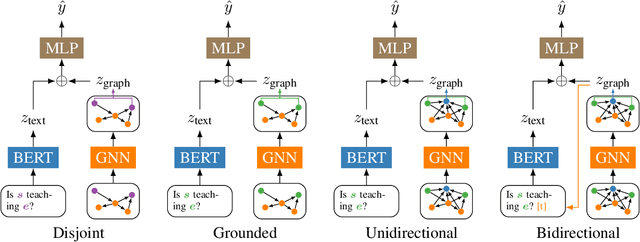
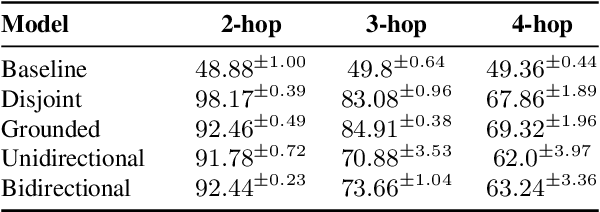
Grounded language models use external sources of information, such as knowledge graphs, to meet some of the general challenges associated with pre-training. By extending previous work on compositional generalization in semantic parsing, we allow for a controlled evaluation of the degree to which these models learn and generalize from patterns in knowledge graphs. We develop a procedure for generating natural language questions paired with knowledge graphs that targets different aspects of compositionality and further avoids grounding the language models in information already encoded implicitly in their weights. We evaluate existing methods for combining language models with knowledge graphs and find them to struggle with generalization to sequences of unseen lengths and to novel combinations of seen base components. While our experimental results provide some insight into the expressive power of these models, we hope our work and released datasets motivate future research on how to better combine language models with structured knowledge representations.

On the Correspondence Between Monotonic Max-Sum GNNs and Datalog

Although there has been significant interest in applying machine learning techniques to structured data, the expressivity (i.e., a description of what can be learned) of such techniques is still poorly understood. In this paper, we study data transformations based on graph neural networks (GNNs). First, we note that the choice of how a dataset is encoded into a numeric form processable by a GNN can obscure the characterisation of a model's expressivity, and we argue that a canonical encoding provides an appropriate basis. Second, we study the expressivity of monotonic max-sum GNNs, which cover a subclass of GNNs with max and sum aggregation functions. We show that, for each such GNN, one can compute a Datalog program such that applying the GNN to any dataset produces the same facts as a single round of application of the program's rules to the dataset. Monotonic max-sum GNNs can sum an unbounded number of feature vectors which can result in arbitrarily large feature values, whereas rule application requires only a bounded number of constants. Hence, our result shows that the unbounded summation of monotonic max-sum GNNs does not increase their expressive power. Third, we sharpen our result to the subclass of monotonic max GNNs, which use only the max aggregation function, and identify a corresponding class of Datalog programs.

Revisiting Inferential Benchmarks for Knowledge Graph Completion

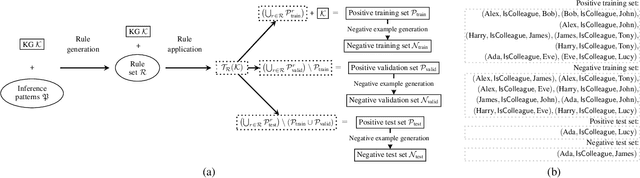
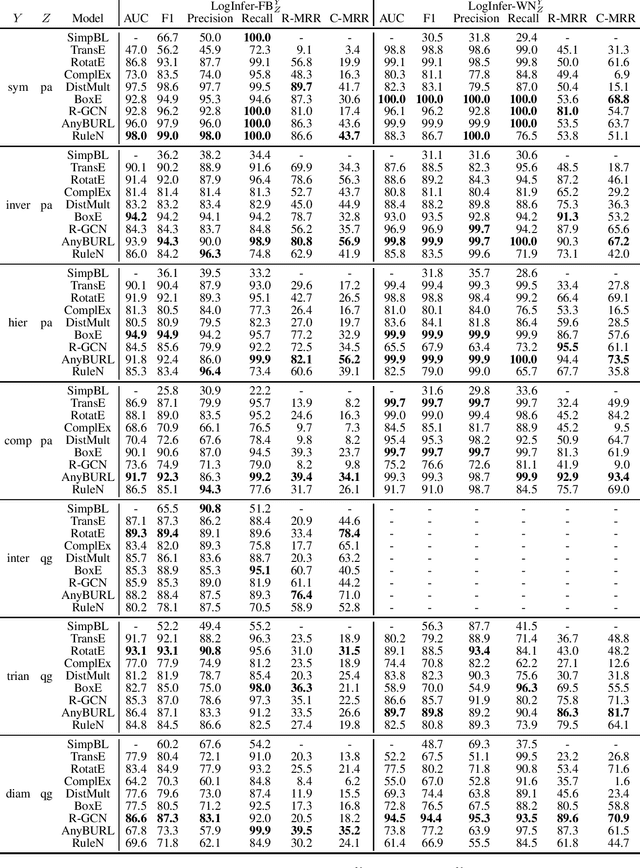
Knowledge Graph (KG) completion is the problem of extending an incomplete KG with missing facts. A key feature of Machine Learning approaches for KG completion is their ability to learn inference patterns, so that the predicted facts are the results of applying these patterns to the KG. Standard completion benchmarks, however, are not well-suited for evaluating models' abilities to learn patterns, because the training and test sets of these benchmarks are a random split of a given KG and hence do not capture the causality of inference patterns. We propose a novel approach for designing KG completion benchmarks based on the following principles: there is a set of logical rules so that the missing facts are the results of the rules' application; the training set includes both premises matching rule antecedents and the corresponding conclusions; the test set consists of the results of applying the rules to the training set; the negative examples are designed to discourage the models from learning rules not entailed by the rule set. We use our methodology to generate several benchmarks and evaluate a wide range of existing KG completion systems. Our results provide novel insights on the ability of existing models to induce inference patterns from incomplete KGs.

Towards Ontology Reshaping for KG Generation with User-in-the-Loop: Applied to Bosch Welding

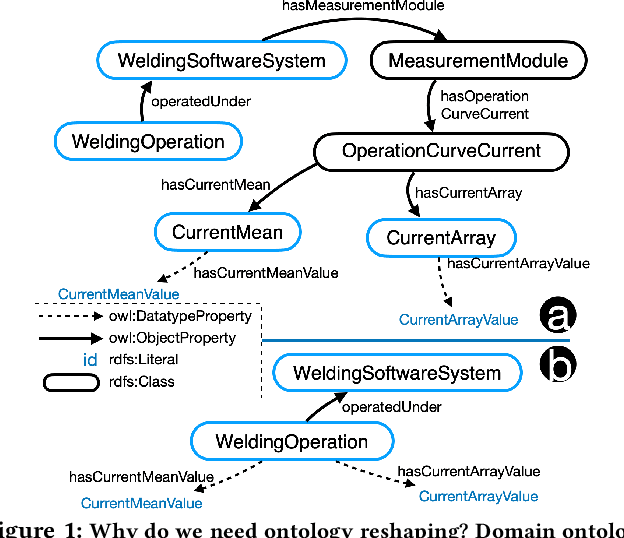
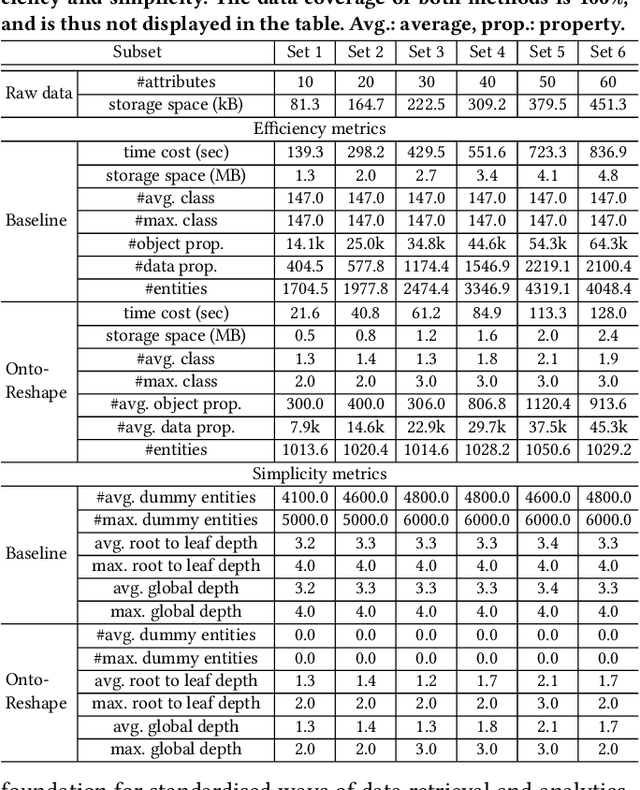
Knowledge graphs (KG) are used in a wide range of applications. The automation of KG generation is very desired due to the data volume and variety in industries. One important approach of KG generation is to map the raw data to a given KG schema, namely a domain ontology, and construct the entities and properties according to the ontology. However, the automatic generation of such ontology is demanding and existing solutions are often not satisfactory. An important challenge is a trade-off between two principles of ontology engineering: knowledge-orientation and data-orientation. The former one prescribes that an ontology should model the general knowledge of a domain, while the latter one emphasises on reflecting the data specificities to ensure good usability. We address this challenge by our method of ontology reshaping, which automates the process of converting a given domain ontology to a smaller ontology that serves as the KG schema. The domain ontology can be designed to be knowledge-oriented and the KG schema covers the data specificities. In addition, our approach allows the option of including user preferences in the loop. We demonstrate our on-going research on ontology reshaping and present an evaluation using real industrial data, with promising results.

Stratified Negation in Limit Datalog Programs

There has recently been an increasing interest in declarative data analysis, where analytic tasks are specified using a logical language, and their implementation and optimisation are delegated to a general-purpose query engine. Existing declarative languages for data analysis can be formalised as variants of logic programming equipped with arithmetic function symbols and/or aggregation, and are typically undecidable. In prior work, the language of $\mathit{limit\ programs}$ was proposed, which is sufficiently powerful to capture many analysis tasks and has decidable entailment problem. Rules in this language, however, do not allow for negation. In this paper, we study an extension of limit programs with stratified negation-as-failure. We show that the additional expressive power makes reasoning computationally more demanding, and provide tight data complexity bounds. We also identify a fragment with tractable data complexity and sufficient expressivity to capture many relevant tasks.

Foundations of Declarative Data Analysis Using Limit Datalog Programs

Motivated by applications in declarative data analysis, we study $\mathit{Datalog}_{\mathbb{Z}}$---an extension of positive Datalog with arithmetic functions over integers. This language is known to be undecidable, so we propose two fragments. In $\mathit{limit}~\mathit{Datalog}_{\mathbb{Z}}$ predicates are axiomatised to keep minimal/maximal numeric values, allowing us to show that fact entailment is coNExpTime-complete in combined, and coNP-complete in data complexity. Moreover, an additional $\mathit{stability}$ requirement causes the complexity to drop to ExpTime and PTime, respectively. Finally, we show that stable $\mathit{Datalog}_{\mathbb{Z}}$ can express many useful data analysis tasks, and so our results provide a sound foundation for the development of advanced information systems.

The Bag Semantics of Ontology-Based Data Access

Ontology-based data access (OBDA) is a popular approach for integrating and querying multiple data sources by means of a shared ontology. The ontology is linked to the sources using mappings, which assign views over the data to ontology predicates. Motivated by the need for OBDA systems supporting database-style aggregate queries, we propose a bag semantics for OBDA, where duplicate tuples in the views defined by the mappings are retained, as is the case in standard databases. We show that bag semantics makes conjunctive query answering in OBDA coNP-hard in data complexity. To regain tractability, we consider a rather general class of queries and show its rewritability to a generalisation of the relational calculus to bags.

Controlled Query Evaluation for Datalog and OWL 2 Profile Ontologies

We study confidentiality enforcement in ontologies under the Controlled Query Evaluation framework, where a policy specifies the sensitive information and a censor ensures that query answers that may compromise the policy are not returned. We focus on censors that ensure confidentiality while maximising information access, and consider both Datalog and the OWL 2 profiles as ontology languages.