David Tena Cucala
On the Correspondence Between Monotonic Max-Sum GNNs and Datalog
Jun 15, 2023Abstract:Although there has been significant interest in applying machine learning techniques to structured data, the expressivity (i.e., a description of what can be learned) of such techniques is still poorly understood. In this paper, we study data transformations based on graph neural networks (GNNs). First, we note that the choice of how a dataset is encoded into a numeric form processable by a GNN can obscure the characterisation of a model's expressivity, and we argue that a canonical encoding provides an appropriate basis. Second, we study the expressivity of monotonic max-sum GNNs, which cover a subclass of GNNs with max and sum aggregation functions. We show that, for each such GNN, one can compute a Datalog program such that applying the GNN to any dataset produces the same facts as a single round of application of the program's rules to the dataset. Monotonic max-sum GNNs can sum an unbounded number of feature vectors which can result in arbitrarily large feature values, whereas rule application requires only a bounded number of constants. Hence, our result shows that the unbounded summation of monotonic max-sum GNNs does not increase their expressive power. Third, we sharpen our result to the subclass of monotonic max GNNs, which use only the max aggregation function, and identify a corresponding class of Datalog programs.
Consequence-based Reasoning for Description Logics with Disjunction, Inverse Roles, Number Restrictions, and Nominals
May 03, 2018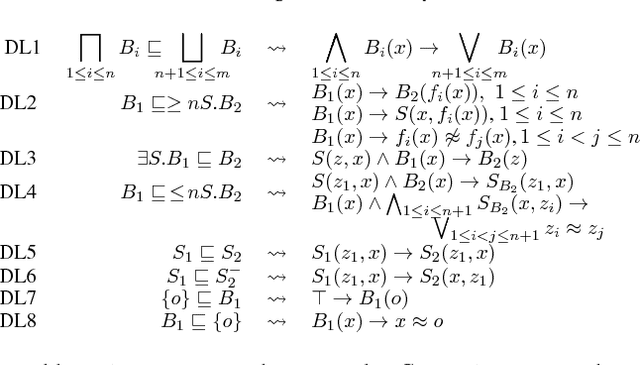


Abstract:We present a consequence-based calculus for concept subsumption and classification in the description logic ALCHOIQ, which extends ALC with role hierarchies, inverse roles, number restrictions, and nominals. By using standard transformations, our calculus extends to SROIQ, which covers all of OWL 2 DL except for datatypes. A key feature of our calculus is its pay-as-you-go behaviour: unlike existing algorithms, our calculus is worst-case optimal for all the well-known proper fragments of ALCHOIQ, albeit not for the full logic.
 Add to Chrome
Add to Chrome Add to Firefox
Add to Firefox Add to Edge
Add to Edge