Minimal Explanations for Neural Network Predictions

Explaining neural network predictions is known to be a challenging problem. In this paper, we propose a novel approach which can be effectively exploited, either in isolation or in combination with other methods, to enhance the interpretability of neural model predictions. For a given input to a trained neural model, our aim is to compute a smallest set of input features so that the model prediction changes when these features are disregarded by setting them to an uninformative baseline value. While computing such minimal explanations is computationally intractable in general for fully-connected neural networks, we show that the problem becomes solvable in polynomial time by a greedy algorithm under mild assumptions on the network's activation functions. We then show that our tractability result extends seamlessly to more advanced neural architectures such as convolutional and graph neural networks. We conduct experiments to showcase the capability of our method for identifying the input features that are essential to the model's prediction.

Confronting Machine Learning With Financial Research

This study aims to examine the challenges and applications of machine learning for financial research. Machine learning algorithms have been developed for certain data environments which substantially differ from the one we encounter in finance. Not only do difficulties arise due to some of the idiosyncrasies of financial markets, there is a fundamental tension between the underlying paradigm of machine learning and the research philosophy in financial economics. Given the peculiar features of financial markets and the empirical framework within social science, various adjustments have to be made to the conventional machine learning methodology. We discuss some of the main challenges of machine learning in finance and examine how these could be accounted for. Despite some of the challenges, we argue that machine learning could be unified with financial research to become a robust complement to the econometrician's toolbox. Moreover, we discuss the various applications of machine learning in the research process such as estimation, empirical discovery, testing, causal inference and prediction.

Double-descent curves in neural networks: a new perspective using Gaussian processes

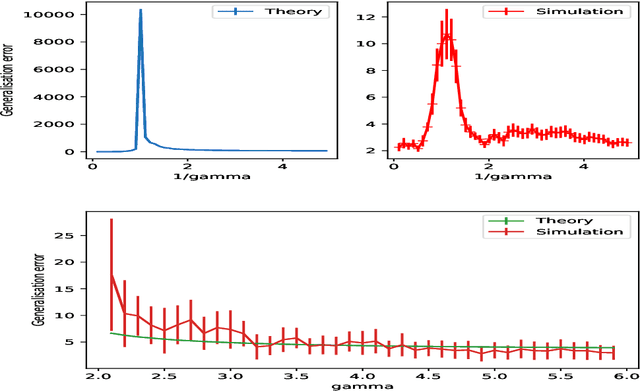
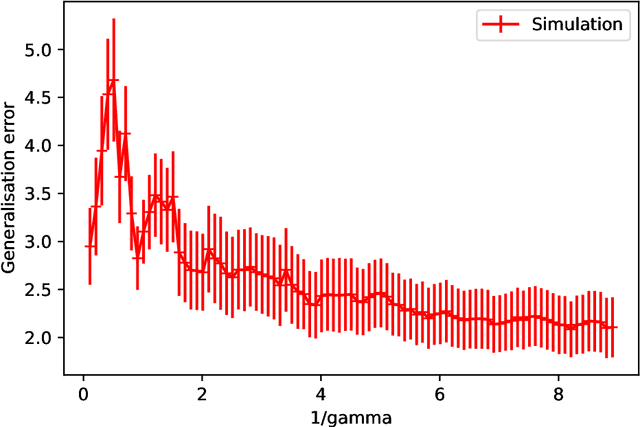
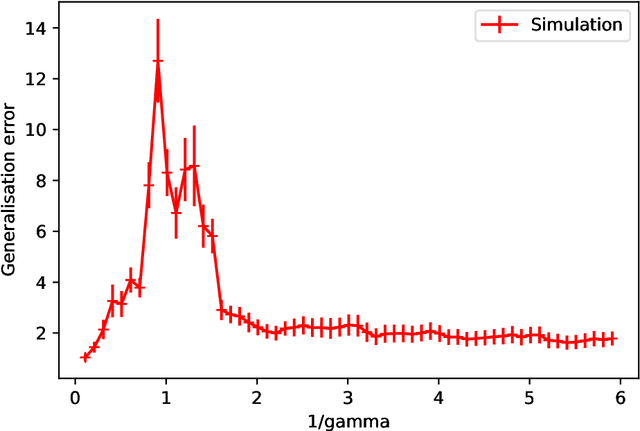
Double-descent curves in neural networks describe the phenomenon that the generalisation error initially descends with increasing parameters, then grows after reaching an optimal number of parameters which is less than the number of data points, but then descends again in the overparameterised regime. Here we use a neural network Gaussian process (NNGP) which maps exactly to a fully connected network (FCN) in the infinite width limit, combined with techniques from random matrix theory, to calculate this generalisation behaviour, with a particular focus on the overparameterised regime. We verify our predictions with numerical simulations of the corresponding Gaussian process regressions. An advantage of our NNGP approach is that the analytical calculations are easier to interpret. We argue that neural network generalization performance improves in the overparameterised regime precisely because that is where they converge to their equivalent Gaussian process.