Do deep neural networks have an inbuilt Occam's razor?

The remarkable performance of overparameterized deep neural networks (DNNs) must arise from an interplay between network architecture, training algorithms, and structure in the data. To disentangle these three components, we apply a Bayesian picture, based on the functions expressed by a DNN, to supervised learning. The prior over functions is determined by the network, and is varied by exploiting a transition between ordered and chaotic regimes. For Boolean function classification, we approximate the likelihood using the error spectrum of functions on data. When combined with the prior, this accurately predicts the posterior, measured for DNNs trained with stochastic gradient descent. This analysis reveals that structured data, combined with an intrinsic Occam's razor-like inductive bias towards (Kolmogorov) simple functions that is strong enough to counteract the exponential growth of the number of functions with complexity, is a key to the success of DNNs.

Transflower: probabilistic autoregressive dance generation with multimodal attention

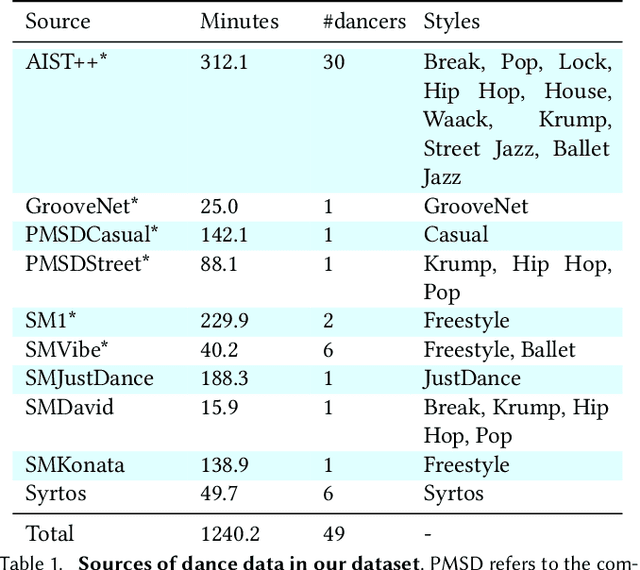
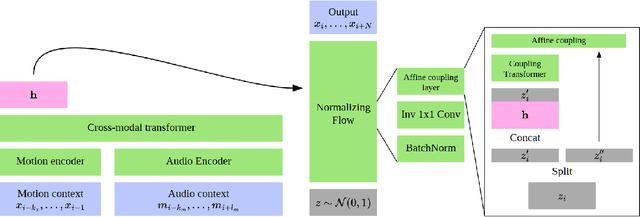
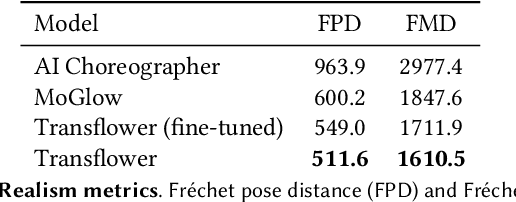
Dance requires skillful composition of complex movements that follow rhythmic, tonal and timbral features of music. Formally, generating dance conditioned on a piece of music can be expressed as a problem of modelling a high-dimensional continuous motion signal, conditioned on an audio signal. In this work we make two contributions to tackle this problem. First, we present a novel probabilistic autoregressive architecture that models the distribution over future poses with a normalizing flow conditioned on previous poses as well as music context, using a multimodal transformer encoder. Second, we introduce the currently largest 3D dance-motion dataset, obtained with a variety of motion-capture technologies, and including both professional and casual dancers. Using this dataset, we compare our new model against two baselines, via objective metrics and a user study, and show that both the ability to model a probability distribution, as well as being able to attend over a large motion and music context are necessary to produce interesting, diverse, and realistic dance that matches the music.

Double-descent curves in neural networks: a new perspective using Gaussian processes

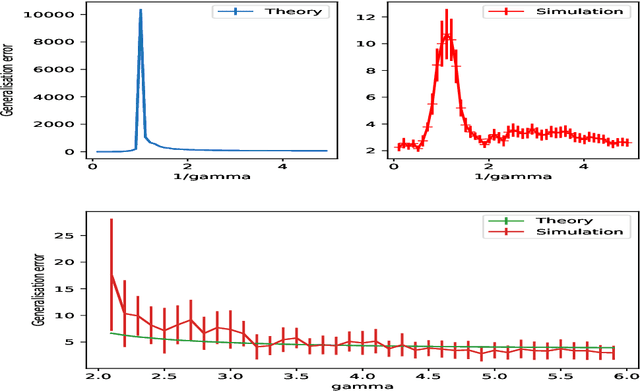
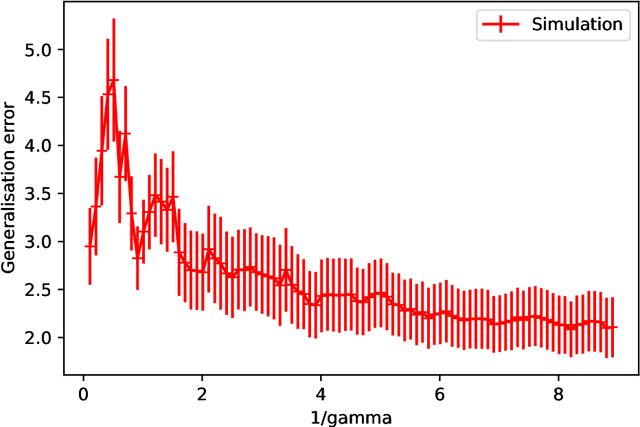
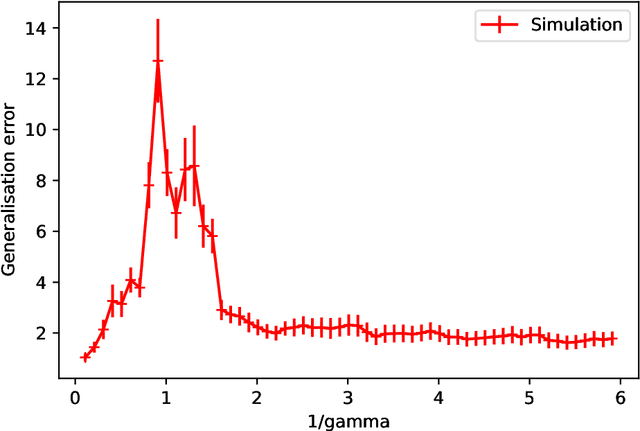
Double-descent curves in neural networks describe the phenomenon that the generalisation error initially descends with increasing parameters, then grows after reaching an optimal number of parameters which is less than the number of data points, but then descends again in the overparameterised regime. Here we use a neural network Gaussian process (NNGP) which maps exactly to a fully connected network (FCN) in the infinite width limit, combined with techniques from random matrix theory, to calculate this generalisation behaviour, with a particular focus on the overparameterised regime. We verify our predictions with numerical simulations of the corresponding Gaussian process regressions. An advantage of our NNGP approach is that the analytical calculations are easier to interpret. We argue that neural network generalization performance improves in the overparameterised regime precisely because that is where they converge to their equivalent Gaussian process.

Generalization bounds for deep learning

Generalization in deep learning has been the topic of much recent theoretical and empirical research. Here we introduce desiderata for techniques that predict generalization errors for deep learning models in supervised learning. Such predictions should 1) scale correctly with data complexity; 2) scale correctly with training set size; 3) capture differences between architectures; 4) capture differences between optimization algorithms; 5) be quantitatively not too far from the true error (in particular, be non-vacuous); 6) be efficiently computable; and 7) be rigorous. We focus on generalization error upper bounds, and introduce a categorisation of bounds depending on assumptions on the algorithm and data. We review a wide range of existing approaches, from classical VC dimension to recent PAC-Bayesian bounds, commenting on how well they perform against the desiderata. We next use a function-based picture to derive a marginal-likelihood PAC-Bayesian bound. This bound is, by one definition, optimal up to a multiplicative constant in the asymptotic limit of large training sets, as long as the learning curve follows a power law, which is typically found in practice for deep learning problems. Extensive empirical analysis demonstrates that our marginal-likelihood PAC-Bayes bound fulfills desiderata 1-3 and 5. The results for 6 and 7 are promising, but not yet fully conclusive, while only desideratum 4 is currently beyond the scope of our bound. Finally, we comment on why this function-based bound performs significantly better than current parameter-based PAC-Bayes bounds.

Is SGD a Bayesian sampler? Well, almost

Overparameterised deep neural networks (DNNs) are highly expressive and so can, in principle, generate almost any function that fits a training dataset with zero error. The vast majority of these functions will perform poorly on unseen data, and yet in practice DNNs often generalise remarkably well. This success suggests that a trained DNN must have a strong inductive bias towards functions with low generalisation error. Here we empirically investigate this inductive bias by calculating, for a range of architectures and datasets, the probability $P_{SGD}(f\mid S)$ that an overparameterised DNN, trained with stochastic gradient descent (SGD) or one of its variants, converges on a function $f$ consistent with a training set $S$. We also use Gaussian processes to estimate the Bayesian posterior probability $P_B(f\mid S)$ that the DNN expresses $f$ upon random sampling of its parameters, conditioned on $S$. Our main findings are that $P_{SGD}(f\mid S)$ correlates remarkably well with $P_B(f\mid S)$ and that $P_B(f\mid S)$ is strongly biased towards low-error and low complexity functions. These results imply that strong inductive bias in the parameter-function map (which determines $P_B(f\mid S)$), rather than a special property of SGD, is the primary explanation for why DNNs generalise so well in the overparameterised regime. While our results suggest that the Bayesian posterior $P_B(f\mid S)$ is the first order determinant of $P_{SGD}(f\mid S)$, there remain second order differences that are sensitive to hyperparameter tuning. A function probability picture, based on $P_{SGD}(f\mid S)$ and/or $P_B(f\mid S)$, can shed new light on the way that variations in architecture or hyperparameter settings such as batch size, learning rate, and optimiser choice, affect DNN performance.

Neural networks are a priori biased towards Boolean functions with low entropy

Understanding the inductive bias of neural networks is critical to explaining their ability to generalise. Here, for one of the simplest neural networks -- a single-layer perceptron with $n$ input neurons, one output neuron, and no threshold bias term -- we prove that upon random initialisation of weights, the a priori probability $P(t)$ that it represents a Boolean function that classifies $t$ points in $\{0,1\}^n$ as $1$ has a remarkably simple form: $ P(t) = 2^{-n} \,\, {\rm for} \,\, 0\leq t < 2^n$. Since a perceptron can express far fewer Boolean functions with small or large values of $t$ (low "entropy") than with intermediate values of $t$ (high "entropy") there is, on average, a strong intrinsic a-priori bias towards individual functions with low entropy. Furthermore, within a class of functions with fixed $t$, we often observe a further intrinsic bias towards functions of lower complexity. Finally, we prove that, regardless of the distribution of inputs, the bias towards low entropy becomes monotonically stronger upon adding ReLU layers, and empirically show that increasing the variance of the bias term has a similar effect.

Deep learning generalizes because the parameter-function map is biased towards simple functions

Deep neural networks generalize remarkably well without explicit regularization even in the strongly over-parametrized regime. This success suggests that some form of implicit regularization must be at work. In this paper we argue that a strong intrinsic bias in the parameter-function map helps explain the success of deep neural networks. We provide evidence that the parameter-function map results in a heavily biased prior over functions, if we assume that the training algorithm samples parameters close to uniformly within the zero-error region. The PAC-Bayes theorem then guarantees good expected generalization for target functions producing high-likelihood training sets. We exploit connections between deep neural networks and Gaussian processes to estimate the marginal likelihood, finding remarkably good agreement between Gaussian processes and neural networks for small input sets. Using approximate marginal likelihood calculations we produce nontrivial generalization PAC-Bayes error bounds which correlate well with the true error on realistic datasets such as MNIST and CIFAR and for architectures including convolutional and fully connected networks. As predicted by recent arguments based on algorithmic information theory, we find that the prior probability drops exponentially with linear increases in several measures of descriptional complexity of the target function. As target functions in many real problems are expected to be highly structured, this simplicity bias offers an insight into why deep networks generalize well on real world problems, but badly on randomized data.