Green My LLM: Studying the key factors affecting the energy consumption of code assistants

In recent years,Large Language Models (LLMs) have significantly improved in generating high-quality code, enabling their integration into developers' Integrated Development Environments (IDEs) as code assistants. These assistants, such as GitHub Copilot, deliver real-time code suggestions and can greatly enhance developers' productivity. However, the environmental impact of these tools, in particular their energy consumption, remains a key concern. This paper investigates the energy consumption of LLM-based code assistants by simulating developer interactions with GitHub Copilot and analyzing various configuration factors. We collected a dataset of development traces from 20 developers and conducted extensive software project development simulations to measure energy usage under different scenarios. Our findings reveal that the energy consumption and performance of code assistants are influenced by various factors, such as the number of concurrent developers, model size, quantization methods, and the use of streaming. Notably, a substantial portion of generation requests made by GitHub Copilot is either canceled or rejected by developers, indicating a potential area for reducing wasted computations. Based on these findings, we share actionable insights into optimizing configurations for different use cases, demonstrating that careful adjustments can lead to significant energy savings.

A Performance Study of LLM-Generated Code on Leetcode

This study evaluates the efficiency of code generation by Large Language Models (LLMs) and measures their performance against human-crafted solutions using a dataset from Leetcode. We compare 18 LLMs, considering factors such as model temperature and success rate, and their impact on code performance. This research introduces a novel method for measuring and comparing the speed of LLM-generated code, revealing that LLMs produce code with comparable performance, irrespective of the adopted LLM. We also find that LLMs are capable of generating code that is, on average, more efficient than the code written by humans. The paper further discusses the use of Leetcode as a benchmarking dataset, the limitations imposed by potential data contamination, and the platform's measurement reliability. We believe that our findings contribute to a better understanding of LLM capabilities in code generation and set the stage for future optimizations in the field.

Pseudo Polynomial-Time Top-k Algorithms for d-DNNF Circuits

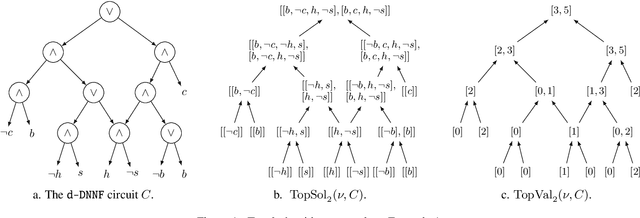
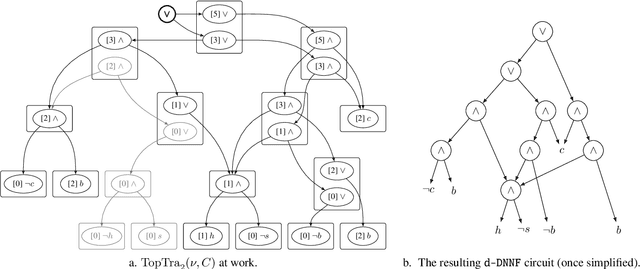
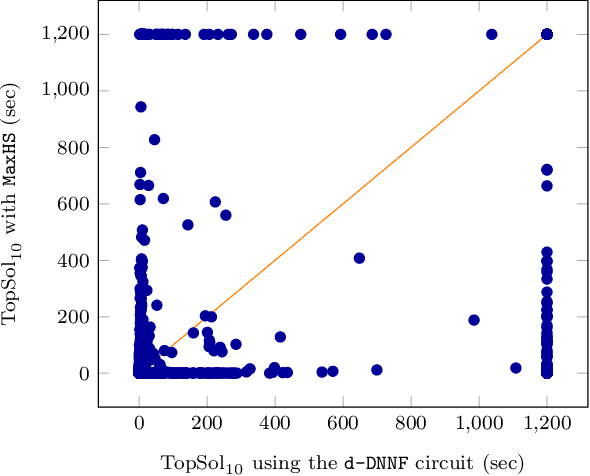
We are interested in computing $k$ most preferred models of a given d-DNNF circuit $C$, where the preference relation is based on an algebraic structure called a monotone, totally ordered, semigroup $(K, \otimes, <)$. In our setting, every literal in $C$ has a value in $K$ and the value of an assignment is an element of $K$ obtained by aggregating using $\otimes$ the values of the corresponding literals. We present an algorithm that computes $k$ models of $C$ among those having the largest values w.r.t. $<$, and show that this algorithm runs in time polynomial in $k$ and in the size of $C$. We also present a pseudo polynomial-time algorithm for deriving the top-$k$ values that can be reached, provided that an additional (but not very demanding) requirement on the semigroup is satisfied. Under the same assumption, we present a pseudo polynomial-time algorithm that transforms $C$ into a d-DNNF circuit $C'$ satisfied exactly by the models of $C$ having a value among the top-$k$ ones. Finally, focusing on the semigroup $(\mathbb{N}, +, <)$, we compare on a large number of instances the performances of our compilation-based algorithm for computing $k$ top solutions with those of an algorithm tackling the same problem, but based on a partial weighted MaxSAT solver.

Feature-Model-Guided Online Learning for Self-Adaptive Systems

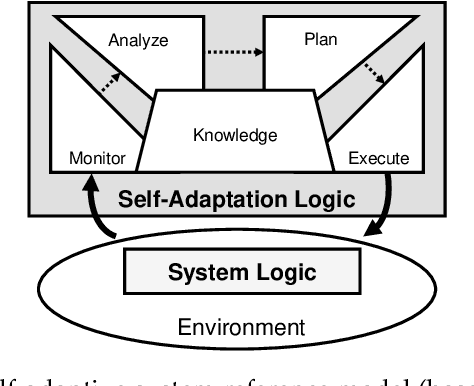
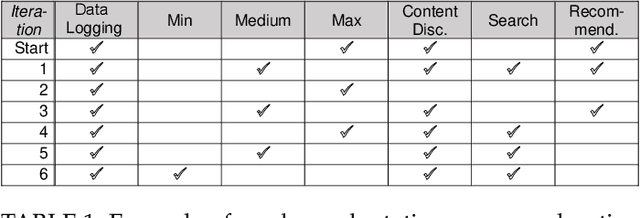
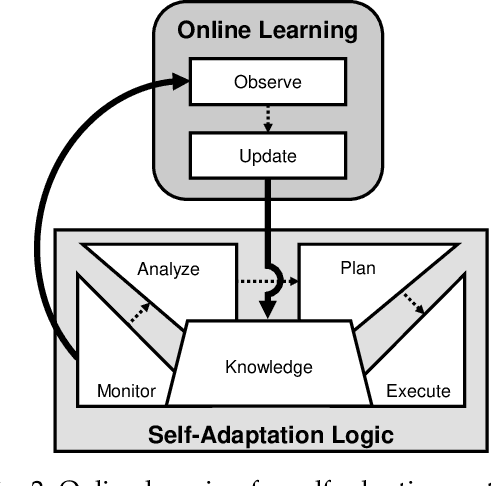
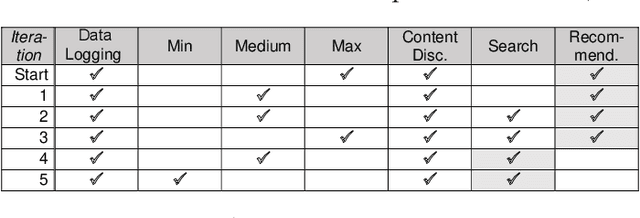
A self-adaptive system can modify its own structure and behavior at runtime based on its perception of the environment, of itself and of its requirements. To develop a self-adaptive system, software developers codify knowledge about the system and its environment, as well as how adaptation actions impact on the system. However, the codified knowledge may be insufficient due to design time uncertainty, and thus a self-adaptive system may execute adaptation actions that do not have the desired effect. Online learning is an emerging approach to address design time uncertainty by employing machine learning at runtime. Online learning accumulates knowledge at runtime by, for instance, exploring not-yet executed adaptation actions. We address two specific problems with respect to online learning for self-adaptive systems. First, the number of possible adaptation actions can be very large. Existing online learning techniques randomly explore the possible adaptation actions, but this can lead to slow convergence of the learning process. Second, the possible adaptation actions can change as a result of system evolution. Existing online learning techniques are unaware of these changes and thus do not explore new adaptation actions, but explore adaptation actions that are no longer valid. We propose using feature models to give structure to the set of adaptation actions and thereby guide the exploration process during online learning. Experimental results involving four real-world systems suggest that considering the hierarchical structure of feature models may speed up convergence by 7.2% on average. Considering the differences between feature models before and after an evolution step may speed up convergence by 64.6% on average. [...]