On Dedicated CDCL Strategies for PB Solvers

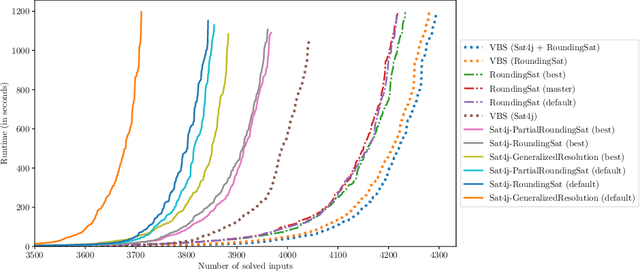
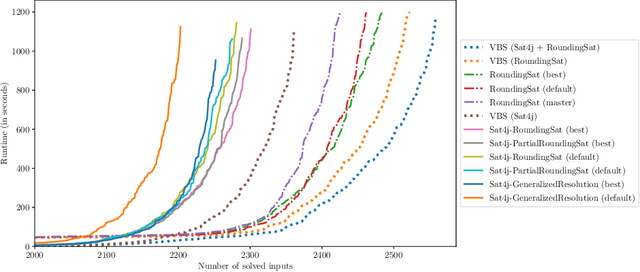
Current implementations of pseudo-Boolean (PB) solvers working on native PB constraints are based on the CDCL architecture which empowers highly efficient modern SAT solvers. In particular, such PB solvers not only implement a (cutting-planes-based) conflict analysis procedure, but also complementary strategies for components that are crucial for the efficiency of CDCL, namely branching heuristics, learned constraint deletion and restarts. However, these strategies are mostly reused by PB solvers without considering the particular form of the PB constraints they deal with. In this paper, we present and evaluate different ways of adapting CDCL strategies to take the specificities of PB constraints into account while preserving the behavior they have in the clausal setting. We implemented these strategies in two different solvers, namely Sat4j (for which we consider three configurations) and RoundingSat. Our experiments show that these dedicated strategies allow to improve, sometimes significantly, the performance of these solvers, both on decision and optimization problems.

On Weakening Strategies for PB Solvers

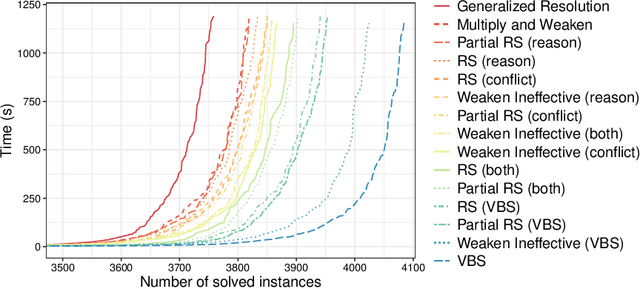
Current pseudo-Boolean solvers implement different variants of the cutting planes proof system to infer new constraints during conflict analysis. One of these variants is generalized resolution, which allows to infer strong constraints, but suffers from the growth of coefficients it generates while combining pseudo-Boolean constraints. Another variant consists in using weakening and division, which is more efficient in practice but may infer weaker constraints. In both cases, weakening is mandatory to derive conflicting constraints. However, its impact on the performance of pseudo-Boolean solvers has not been assessed so far. In this paper, new application strategies for this rule are studied, aiming to infer strong constraints with small coefficients. We implemented them in Sat4j and observed that each of them improves the runtime of the solver. While none of them performs better than the others on all benchmarks, applying weakening on the conflict side has surprising good performance, whereas applying partial weakening and division on both the conflict and the reason sides provides the best results overall.

On the Complexity of Optimization Problems based on Compiled NNF Representations

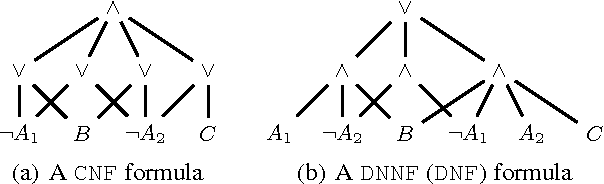
Optimization is a key task in a number of applications. When the set of feasible solutions under consideration is of combinatorial nature and described in an implicit way as a set of constraints, optimization is typically NP-hard. Fortunately, in many problems, the set of feasible solutions does not often change and is independent from the user's request. In such cases, compiling the set of constraints describing the set of feasible solutions during an off-line phase makes sense, if this compilation step renders computationally easier the generation of a non-dominated, yet feasible solution matching the user's requirements and preferences (which are only known at the on-line step). In this article, we focus on propositional constraints. The subsets L of the NNF language analyzed in Darwiche and Marquis' knowledge compilation map are considered. A number of families F of representations of objective functions over propositional variables, including linear pseudo-Boolean functions and more sophisticated ones, are considered. For each language L and each family F, the complexity of generating an optimal solution when the constraints are compiled into L and optimality is to be considered w.r.t. a function from F is identified.

Some thoughts about benchmarks for NMR

The NMR community would like to build a repository of benchmarks to push forward the design of systems implementing NMR as it has been the case for many other areas in AI. There are a number of lessons which can be learned from the experience of other communi- ties. Here are a few thoughts about the requirements and choices to make before building such a repository.