On Dedicated CDCL Strategies for PB Solvers

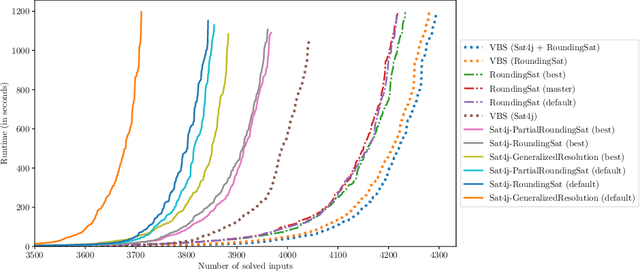
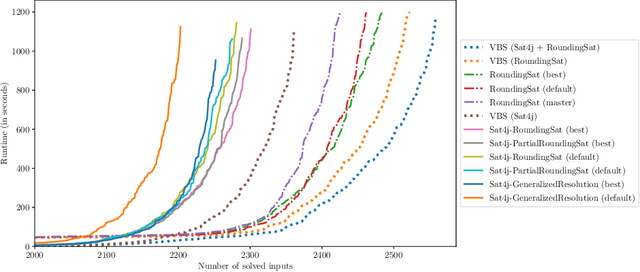
Current implementations of pseudo-Boolean (PB) solvers working on native PB constraints are based on the CDCL architecture which empowers highly efficient modern SAT solvers. In particular, such PB solvers not only implement a (cutting-planes-based) conflict analysis procedure, but also complementary strategies for components that are crucial for the efficiency of CDCL, namely branching heuristics, learned constraint deletion and restarts. However, these strategies are mostly reused by PB solvers without considering the particular form of the PB constraints they deal with. In this paper, we present and evaluate different ways of adapting CDCL strategies to take the specificities of PB constraints into account while preserving the behavior they have in the clausal setting. We implemented these strategies in two different solvers, namely Sat4j (for which we consider three configurations) and RoundingSat. Our experiments show that these dedicated strategies allow to improve, sometimes significantly, the performance of these solvers, both on decision and optimization problems.

On Improving the Backjump Level in PB Solvers

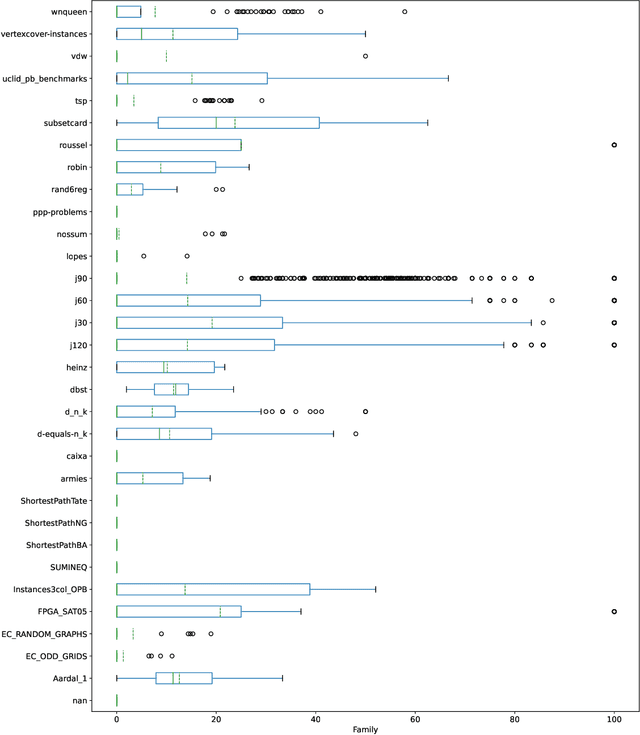
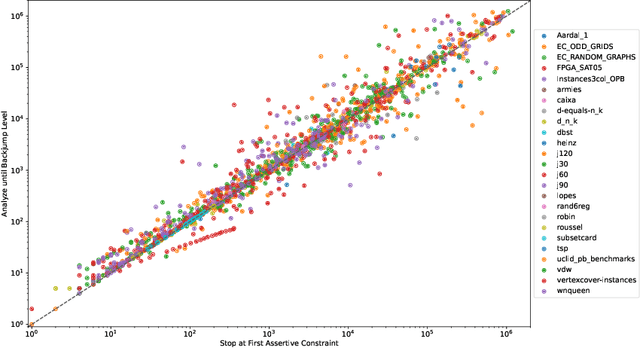
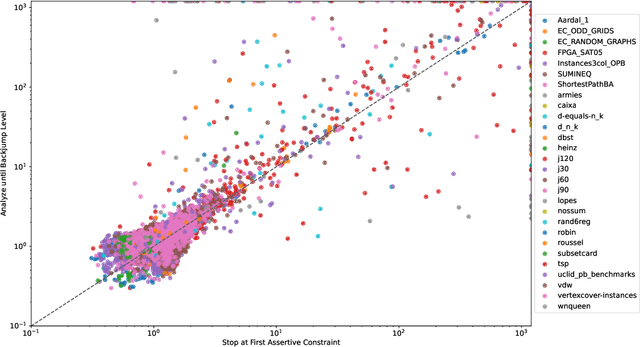
Current PB solvers implement many techniques inspired by the CDCL architecture of modern SAT solvers, so as to benefit from its practical efficiency. However, they also need to deal with the fact that many of the properties leveraged by this architecture are no longer true when considering PB constraints. In this paper, we focus on one of these properties, namely the optimality of the so-called first unique implication point (1-UIP). While it is well known that learning the first assertive clause produced during conflict analysis ensures to perform the highest possible backjump in a SAT solver, we show that there is no such guarantee in the presence of PB constraints. We also introduce and evaluate different approaches designed to improve the backjump level identified during conflict analysis by allowing to continue the analysis after reaching the 1-UIP. Our experiments show that sub-optimal backjumps are fairly common in PB solvers, even though their impact on the solver is not clear.

On Irrelevant Literals in Pseudo-Boolean Constraint Learning

Learning pseudo-Boolean (PB) constraints in PB solvers exploiting cutting planes based inference is not as well understood as clause learning in conflict-driven clause learning solvers. In this paper, we show that PB constraints derived using cutting planes may contain \emph{irrelevant literals}, i.e., literals whose assigned values (whatever they are) never change the truth value of the constraint. Such literals may lead to infer constraints that are weaker than they should be, impacting the size of the proof built by the solver, and thus also affecting its performance. This suggests that current implementations of PB solvers based on cutting planes should be reconsidered to prevent the generation of irrelevant literals. Indeed, detecting and removing irrelevant literals is too expensive in practice to be considered as an option (the associated problem is NP-hard.

On Weakening Strategies for PB Solvers

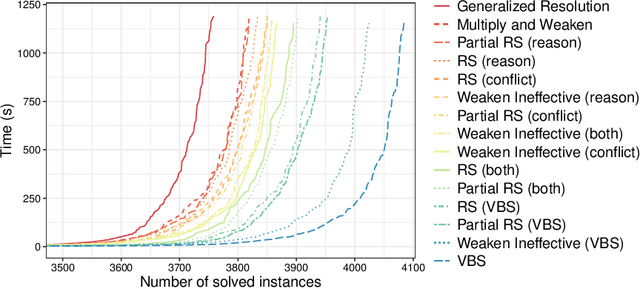
Current pseudo-Boolean solvers implement different variants of the cutting planes proof system to infer new constraints during conflict analysis. One of these variants is generalized resolution, which allows to infer strong constraints, but suffers from the growth of coefficients it generates while combining pseudo-Boolean constraints. Another variant consists in using weakening and division, which is more efficient in practice but may infer weaker constraints. In both cases, weakening is mandatory to derive conflicting constraints. However, its impact on the performance of pseudo-Boolean solvers has not been assessed so far. In this paper, new application strategies for this rule are studied, aiming to infer strong constraints with small coefficients. We implemented them in Sat4j and observed that each of them improves the runtime of the solver. While none of them performs better than the others on all benchmarks, applying weakening on the conflict side has surprising good performance, whereas applying partial weakening and division on both the conflict and the reason sides provides the best results overall.

Revisiting Graph Width Measures for CNF-Encodings

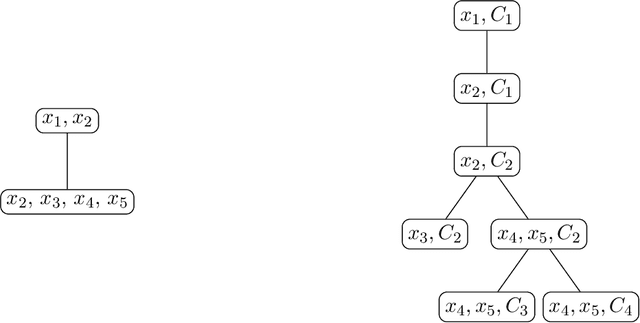
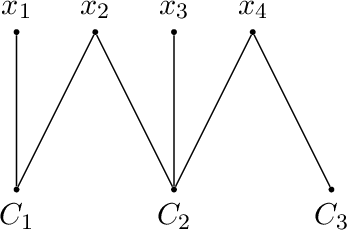
We consider bounded width CNF-formulas where the width is measured by popular graph width measures on graphs associated to CNF-formulas. Such restricted graph classes, in particular those of bounded treewidth, have been extensively studied for their uses in the design of algorithms for various computational problems on CNF-formulas. Here we consider the expressivity of these formulas in the model of clausal encodings with auxiliary variables. We first show that bounding the width for many of the measures from the literature leads to a dramatic loss of expressivity, restricting the formulas to such of low communication complexity. We then show that the width of optimal encodings with respect to different measures is strongly linked: there are two classes of width measures, one containing primal treewidth and the other incidence cliquewidth, such that in each class the width of optimal encodings only differs by constant factors. Moreover, between the two classes the width differs at most by a factor logarithmic in the number of variables. Both these results are in stark contrast to the setting without auxiliary variables where all width measures we consider here differ by more than constant factors and in many cases even by linear factors.