Louenas Bounia
On the Explanatory Power of Decision Trees
Sep 04, 2021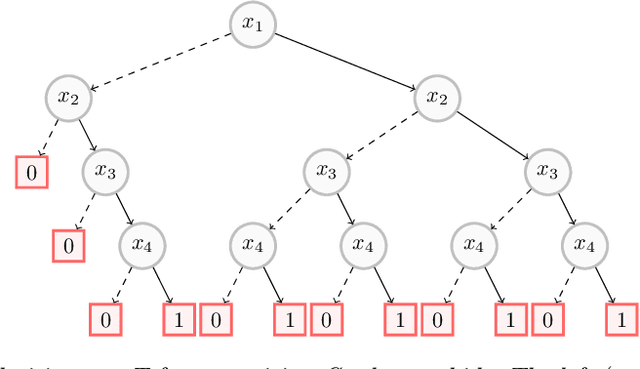
Abstract:Decision trees have long been recognized as models of choice in sensitive applications where interpretability is of paramount importance. In this paper, we examine the computational ability of Boolean decision trees in deriving, minimizing, and counting sufficient reasons and contrastive explanations. We prove that the set of all sufficient reasons of minimal size for an instance given a decision tree can be exponentially larger than the size of the input (the instance and the decision tree). Therefore, generating the full set of sufficient reasons can be out of reach. In addition, computing a single sufficient reason does not prove enough in general; indeed, two sufficient reasons for the same instance may differ on many features. To deal with this issue and generate synthetic views of the set of all sufficient reasons, we introduce the notions of relevant features and of necessary features that characterize the (possibly negated) features appearing in at least one or in every sufficient reason, and we show that they can be computed in polynomial time. We also introduce the notion of explanatory importance, that indicates how frequent each (possibly negated) feature is in the set of all sufficient reasons. We show how the explanatory importance of a feature and the number of sufficient reasons can be obtained via a model counting operation, which turns out to be practical in many cases. We also explain how to enumerate sufficient reasons of minimal size. We finally show that, unlike sufficient reasons, the set of all contrastive explanations for an instance given a decision tree can be derived, minimized and counted in polynomial time.
Trading Complexity for Sparsity in Random Forest Explanations
Aug 11, 2021
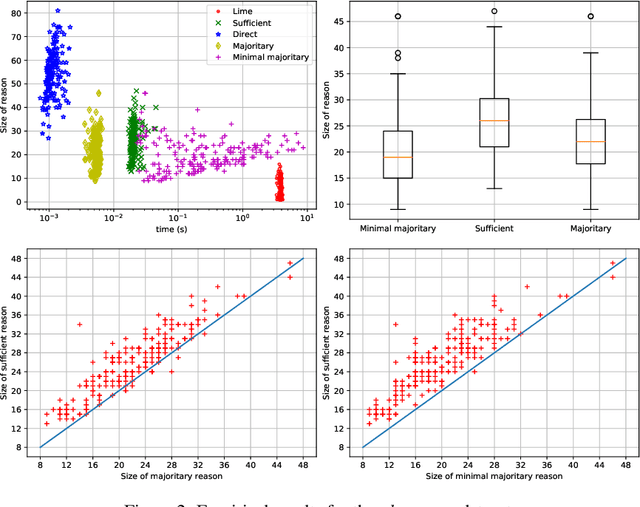
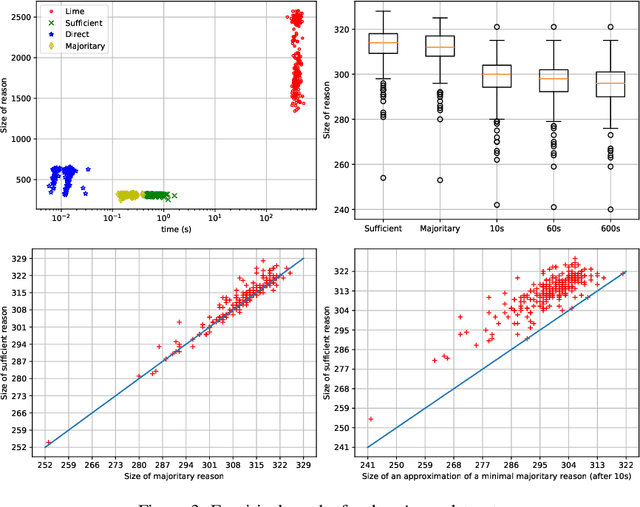
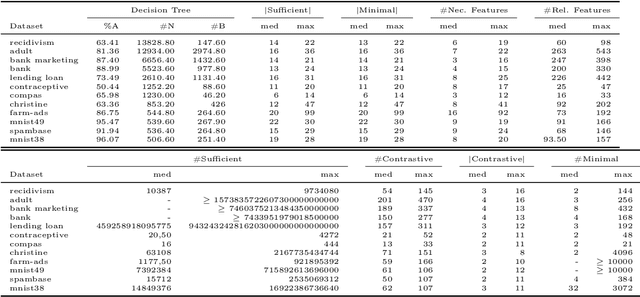
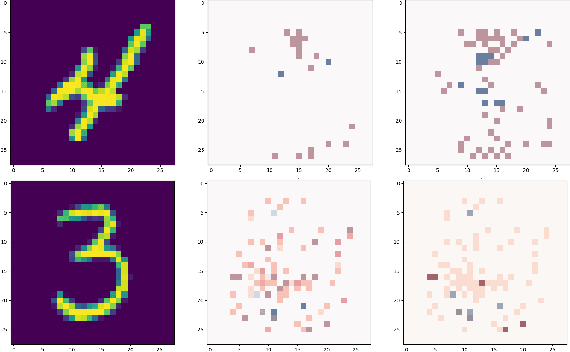
Abstract:Random forests have long been considered as powerful model ensembles in machine learning. By training multiple decision trees, whose diversity is fostered through data and feature subsampling, the resulting random forest can lead to more stable and reliable predictions than a single decision tree. This however comes at the cost of decreased interpretability: while decision trees are often easily interpretable, the predictions made by random forests are much more difficult to understand, as they involve a majority vote over hundreds of decision trees. In this paper, we examine different types of reasons that explain "why" an input instance is classified as positive or negative by a Boolean random forest. Notably, as an alternative to sufficient reasons taking the form of prime implicants of the random forest, we introduce majoritary reasons which are prime implicants of a strict majority of decision trees. For these different abductive explanations, the tractability of the generation problem (finding one reason) and the minimization problem (finding one shortest reason) are investigated. Experiments conducted on various datasets reveal the existence of a trade-off between runtime complexity and sparsity. Sufficient reasons - for which the identification problem is DP-complete - are slightly larger than majoritary reasons that can be generated using a simple linear- time greedy algorithm, and significantly larger than minimal majoritary reasons that can be approached using an anytime P ARTIAL M AX SAT algorithm.
On the Computational Intelligibility of Boolean Classifiers
Apr 13, 2021
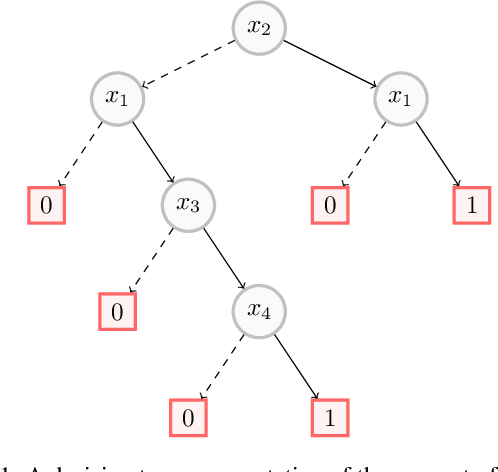
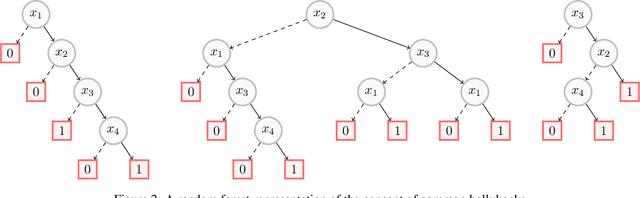

Abstract:In this paper, we investigate the computational intelligibility of Boolean classifiers, characterized by their ability to answer XAI queries in polynomial time. The classifiers under consideration are decision trees, DNF formulae, decision lists, decision rules, tree ensembles, and Boolean neural nets. Using 9 XAI queries, including both explanation queries and verification queries, we show the existence of large intelligibility gap between the families of classifiers. On the one hand, all the 9 XAI queries are tractable for decision trees. On the other hand, none of them is tractable for DNF formulae, decision lists, random forests, boosted decision trees, Boolean multilayer perceptrons, and binarized neural networks.
 Add to Chrome
Add to Chrome Add to Firefox
Add to Firefox Add to Edge
Add to Edge