XCSP3: An Integrated Format for Benchmarking Combinatorial Constrained Problems

We propose a major revision of the format XCSP 2.1, called XCSP3, to build integrated representations of combinatorial constrained problems. This new format is able to deal with mono/multi optimization, many types of variables, cost functions, reification, views, annotations, variable quantification, distributed, probabilistic and qualitative reasoning. The new format is made compact, highly readable, and rather easy to parse. Interestingly, it captures the structure of the problem models, through the possibilities of declaring arrays of variables, and identifying syntactic and semantic groups of constraints. The number of constraints is kept under control by introducing a limited set of basic constraint forms, and producing almost automatically some of their variations through lifting, restriction, sliding, logical combination and relaxation mechanisms. As a result, XCSP3 encompasses practically all constraints that can be found in major constraint solvers developed by the CP community. A website, which is developed conjointly with the format, contains many models and series of instances. The user can make sophisticated queries for selecting instances from very precise criteria. The objective of XCSP3 is to ease the effort required to test and compare different algorithms by providing a common test-bed of combinatorial constrained instances.

A Simple Model to Generate Hard Satisfiable Instances

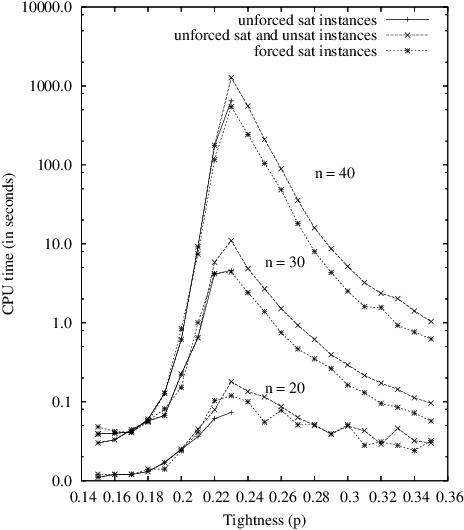
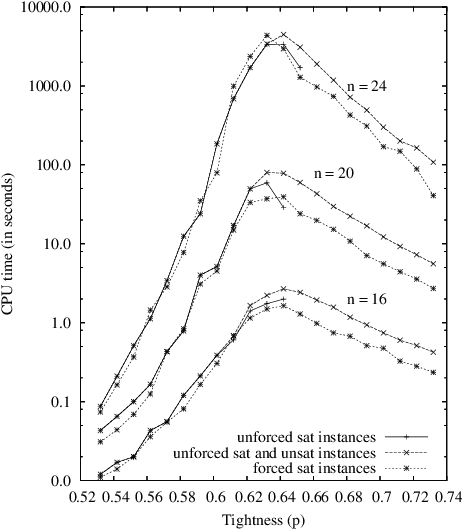
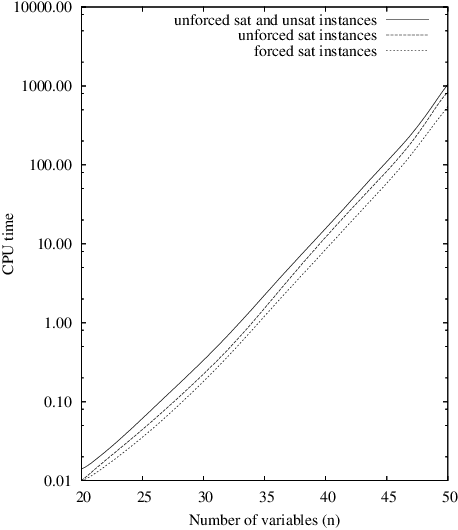
In this paper, we try to further demonstrate that the models of random CSP instances proposed by [Xu and Li, 2000; 2003] are of theoretical and practical interest. Indeed, these models, called RB and RD, present several nice features. First, it is quite easy to generate random instances of any arity since no particular structure has to be integrated, or property enforced, in such instances. Then, the existence of an asymptotic phase transition can be guaranteed while applying a limited restriction on domain size and on constraint tightness. In that case, a threshold point can be precisely located and all instances have the guarantee to be hard at the threshold, i.e., to have an exponential tree-resolution complexity. Next, a formal analysis shows that it is possible to generate forced satisfiable instances whose hardness is similar to unforced satisfiable ones. This analysis is supported by some representative results taken from an intensive experimentation that we have carried out, using complete and incomplete search methods.