A Simple Model to Generate Hard Satisfiable Instances
Paper and Code
Sep 12, 2005
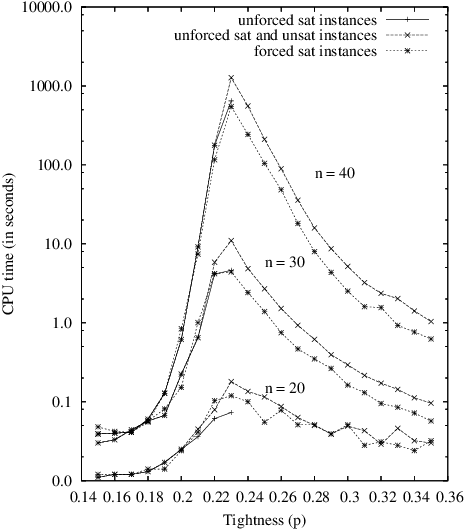
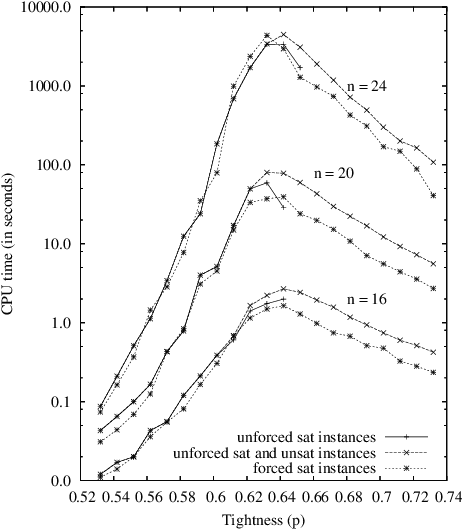
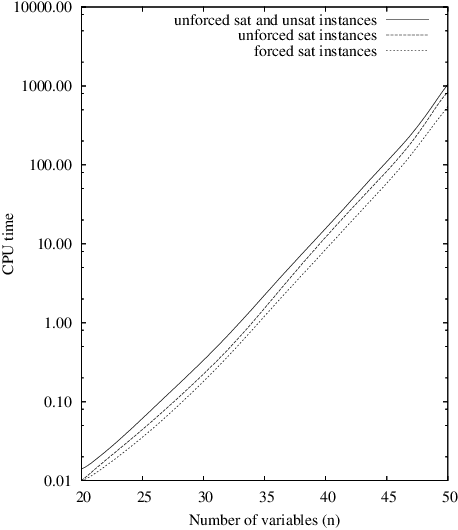
In this paper, we try to further demonstrate that the models of random CSP instances proposed by [Xu and Li, 2000; 2003] are of theoretical and practical interest. Indeed, these models, called RB and RD, present several nice features. First, it is quite easy to generate random instances of any arity since no particular structure has to be integrated, or property enforced, in such instances. Then, the existence of an asymptotic phase transition can be guaranteed while applying a limited restriction on domain size and on constraint tightness. In that case, a threshold point can be precisely located and all instances have the guarantee to be hard at the threshold, i.e., to have an exponential tree-resolution complexity. Next, a formal analysis shows that it is possible to generate forced satisfiable instances whose hardness is similar to unforced satisfiable ones. This analysis is supported by some representative results taken from an intensive experimentation that we have carried out, using complete and incomplete search methods.
 Add to Chrome
Add to Chrome Add to Firefox
Add to Firefox Add to Edge
Add to Edge