Robust And Scalable Learning Of Complex Dataset Topologies Via Elpigraph
Paper and Code
Jun 20, 2018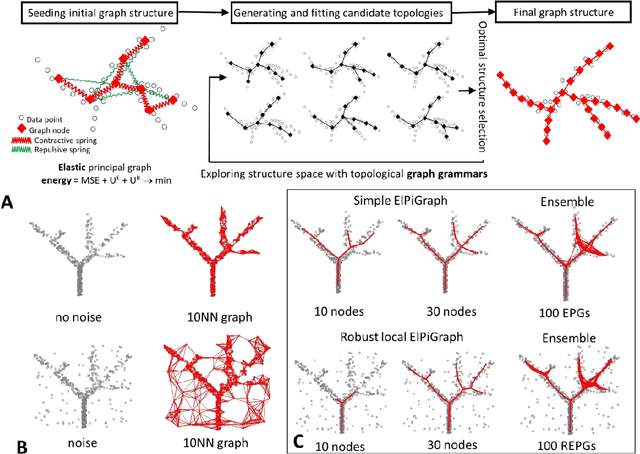
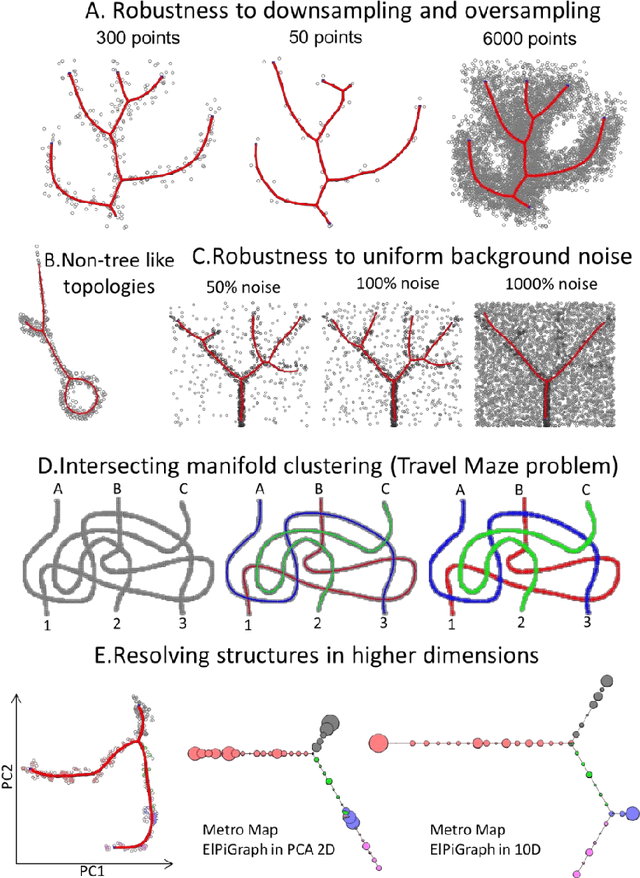
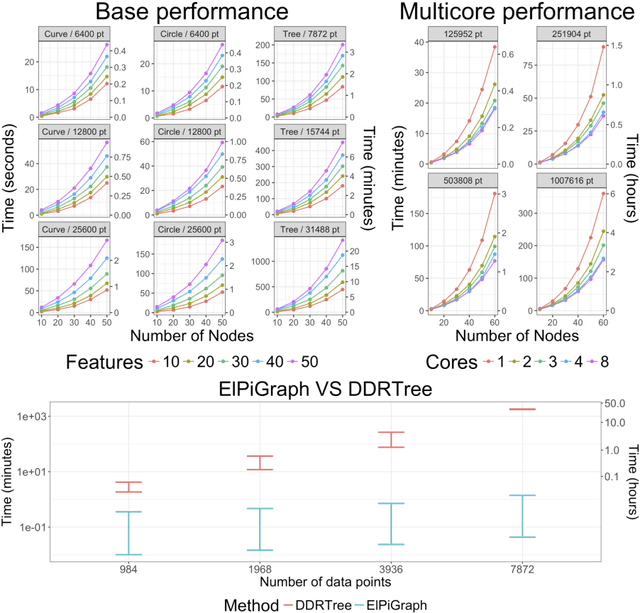
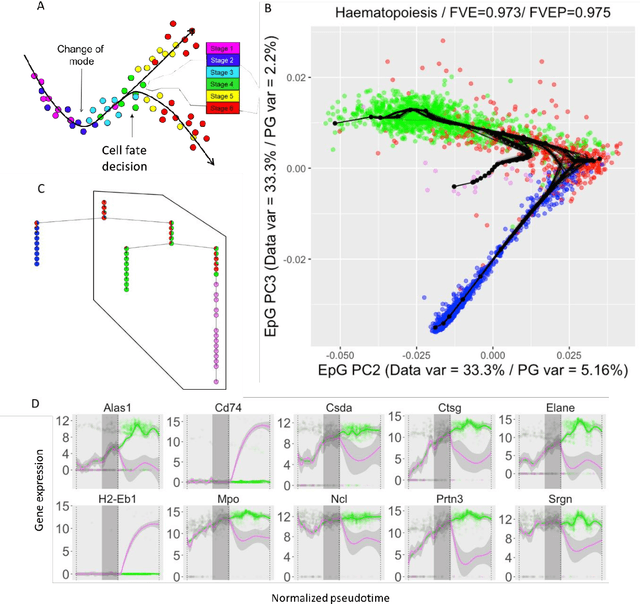
Large datasets represented by multidimensional data point clouds often possess non-trivial distributions with branching trajectories and excluded regions, with the recent single-cell transcriptomic studies of developing embryo being notable examples. Reducing the complexity and producing compact and interpretable representations of such data remains a challenging task. Most of the existing computational methods are based on exploring the local data point neighbourhood relations, a step that can perform poorly in the case of multidimensional and noisy data. Here we present ElPiGraph, a scalable and robust method for approximation of datasets with complex structures which does not require computing the complete data distance matrix or the data point neighbourhood graph. This method is able to withstand high levels of noise and is capable of approximating complex topologies via principal graph ensembles that can be combined into a consensus principal graph. ElPiGraph deals efficiently with large and complex datasets in various fields from biology, where it can be used to infer gene dynamics from single-cell RNA-Seq, to astronomy, where it can be used to explore complex structures in the distribution of galaxies.
 Add to Chrome
Add to Chrome Add to Firefox
Add to Firefox Add to Edge
Add to Edge