Similarity-based prediction of Ejection Fraction in Heart Failure Patients

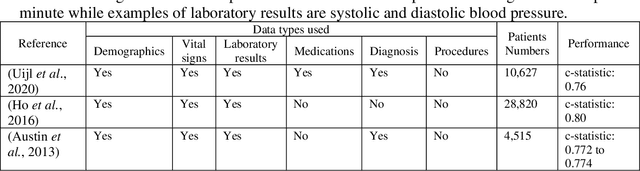
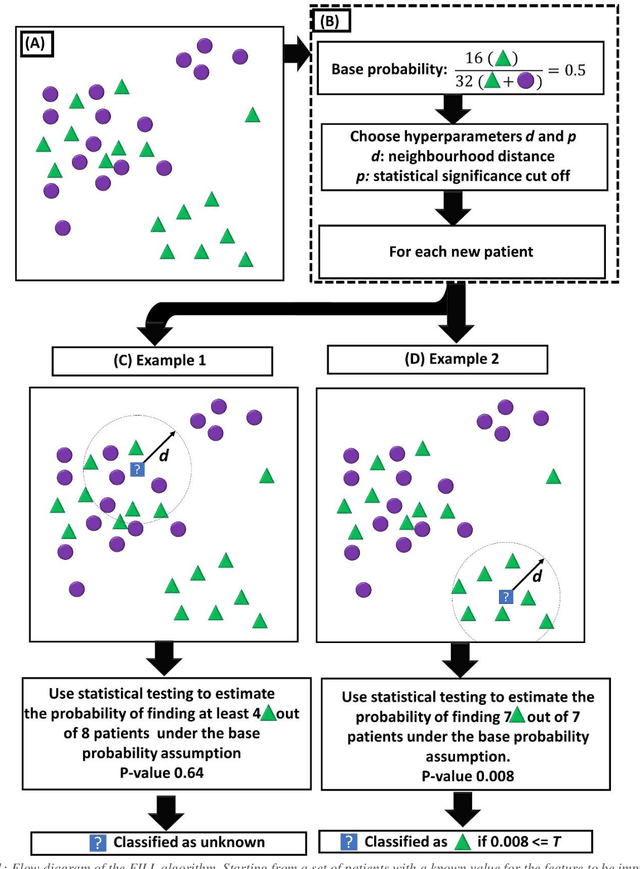
Biomedical research is increasingly employing real world evidence (RWE) to foster discoveries of novel clinical phenotypes and to better characterize long term effect of medical treatments. However, due to limitations inherent in the collection process, RWE often lacks key features of patients, particularly when these features cannot be directly encoded using data standards such as ICD-10. Here we propose a novel data-driven statistical machine learning approach, named Feature Imputation via Local Likelihood (FILL), designed to infer missing features by exploiting feature similarity between patients. We test our method using a particularly challenging problem: differentiating heart failure patients with reduced versus preserved ejection fraction (HFrEF and HFpEF respectively). The complexity of the task stems from three aspects: the two share many common characteristics and treatments, only part of the relevant diagnoses may have been recorded, and the information on ejection fraction is often missing from RWE datasets. Despite these difficulties, our method is shown to be capable of inferring heart failure patients with HFpEF with a precision above 80% when considering multiple scenarios across two RWE datasets containing 11,950 and 10,051 heart failure patients. This is an improvement when compared to classical approaches such as logistic regression and random forest which were only able to achieve a precision < 73%. Finally, this approach allows us to analyse which features are commonly associated with HFpEF patients. For example, we found that specific diagnostic codes for atrial fibrillation and personal history of long-term use of anticoagulants are often key in identifying HFpEF patients.

Deep Semi-Supervised Embedded Clustering (DSEC) for Stratification of Heart Failure Patients

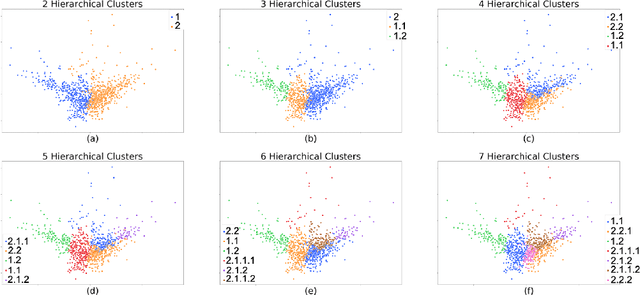
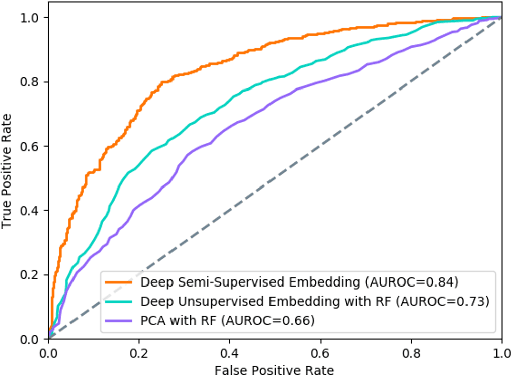
Determining phenotypes of diseases can have considerable benefits for in-hospital patient care and to drug development. The structure of high dimensional data sets such as electronic health records are often represented through an embedding of the data, with clustering methods used to group data of similar structure. If subgroups are known to exist within data, supervised methods may be used to influence the clusters discovered. We propose to extend deep embedded clustering to a semi-supervised deep embedded clustering algorithm to stratify subgroups through known labels in the data. In this work we apply deep semi-supervised embedded clustering to determine data-driven patient subgroups of heart failure from the electronic health records of 4,487 heart failure and control patients. We find clinically relevant clusters from an embedded space derived from heterogeneous data. The proposed algorithm can potentially find new undiagnosed subgroups of patients that have different outcomes, and, therefore, lead to improved treatments.

Estimating the effective dimension of large biological datasets using Fisher separability analysis

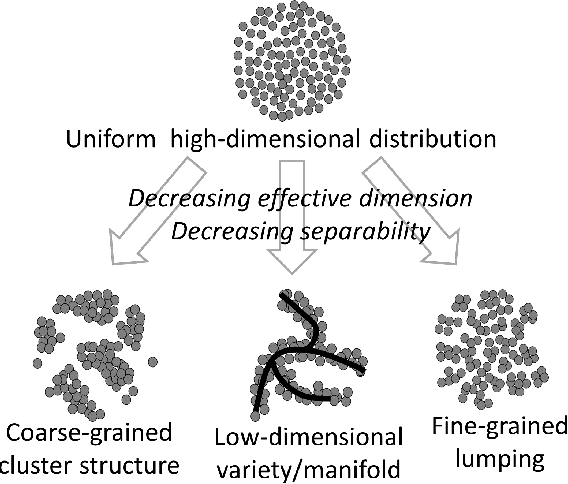
Modern large-scale datasets are frequently said to be high-dimensional. However, their data point clouds frequently possess structures, significantly decreasing their intrinsic dimensionality (ID) due to the presence of clusters, points being located close to low-dimensional varieties or fine-grained lumping. We test a recently introduced dimensionality estimator, based on analysing the separability properties of data points, on several benchmarks and real biological datasets. We show that the introduced measure of ID has performance competitive with state-of-the-art measures, being efficient across a wide range of dimensions and performing better in the case of noisy samples. Moreover, it allows estimating the intrinsic dimension in situations where the intrinsic manifold assumption is not valid.

Robust And Scalable Learning Of Complex Dataset Topologies Via Elpigraph

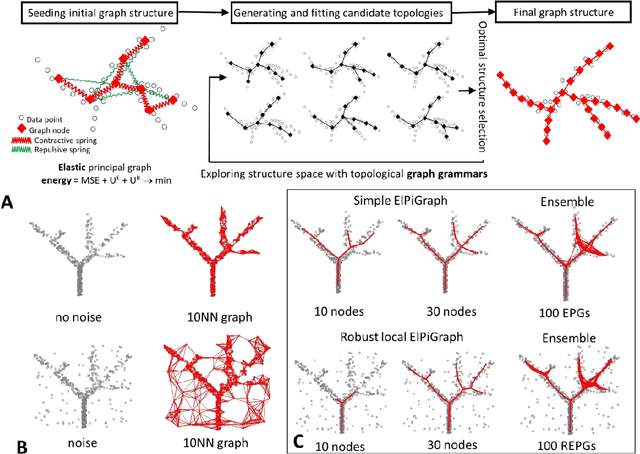
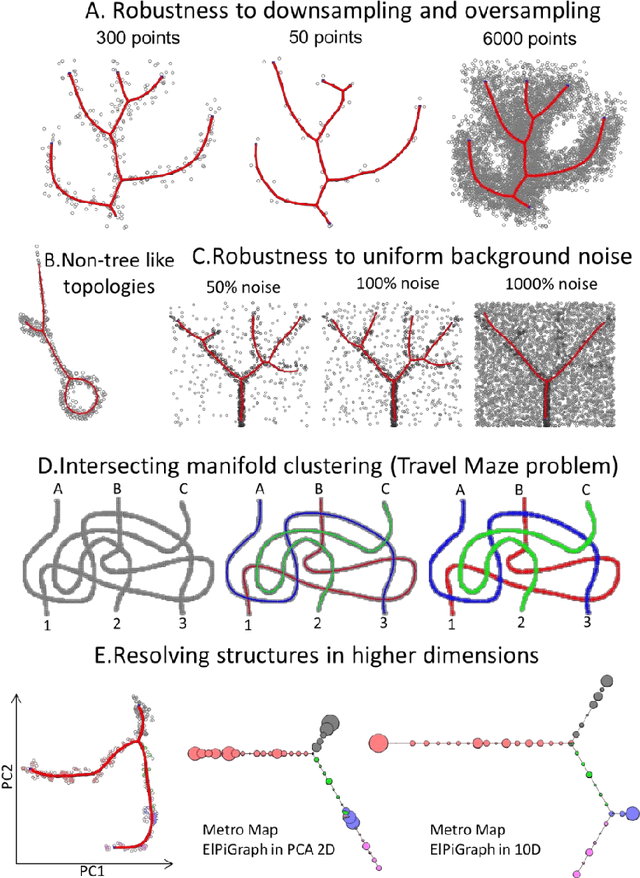
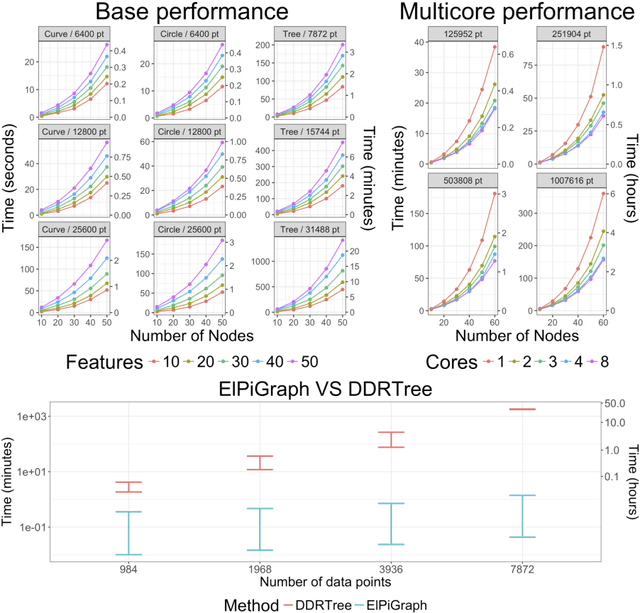
Large datasets represented by multidimensional data point clouds often possess non-trivial distributions with branching trajectories and excluded regions, with the recent single-cell transcriptomic studies of developing embryo being notable examples. Reducing the complexity and producing compact and interpretable representations of such data remains a challenging task. Most of the existing computational methods are based on exploring the local data point neighbourhood relations, a step that can perform poorly in the case of multidimensional and noisy data. Here we present ElPiGraph, a scalable and robust method for approximation of datasets with complex structures which does not require computing the complete data distance matrix or the data point neighbourhood graph. This method is able to withstand high levels of noise and is capable of approximating complex topologies via principal graph ensembles that can be combined into a consensus principal graph. ElPiGraph deals efficiently with large and complex datasets in various fields from biology, where it can be used to infer gene dynamics from single-cell RNA-Seq, to astronomy, where it can be used to explore complex structures in the distribution of galaxies.