Domain Adaptation Principal Component Analysis: base linear method for learning with out-of-distribution data

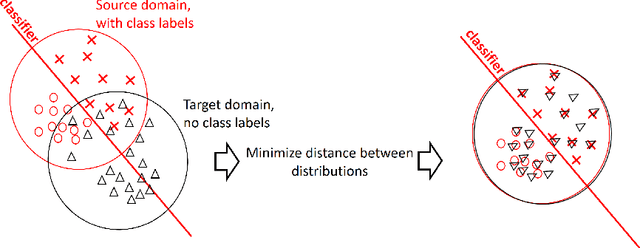
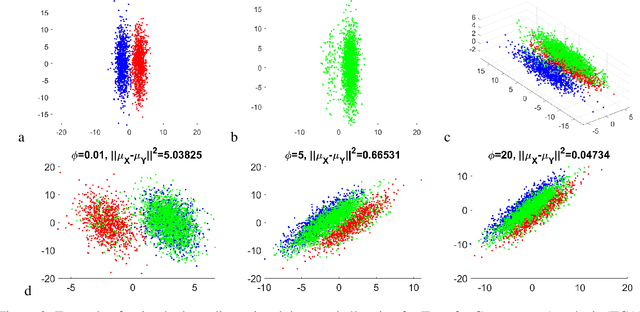
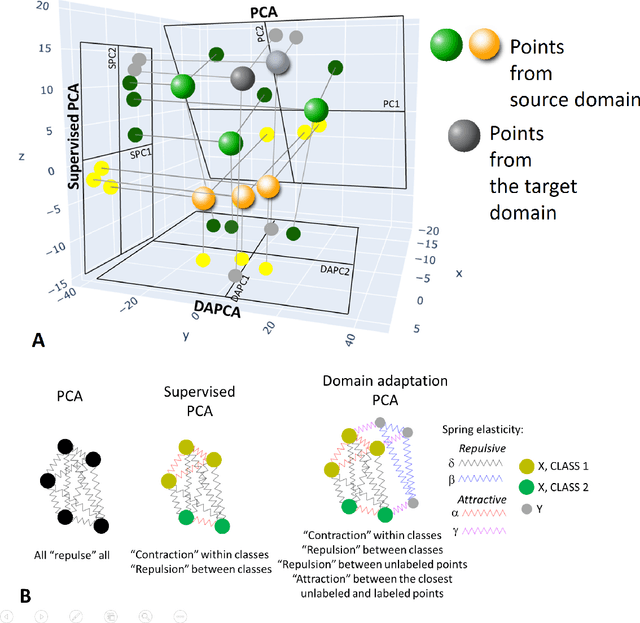
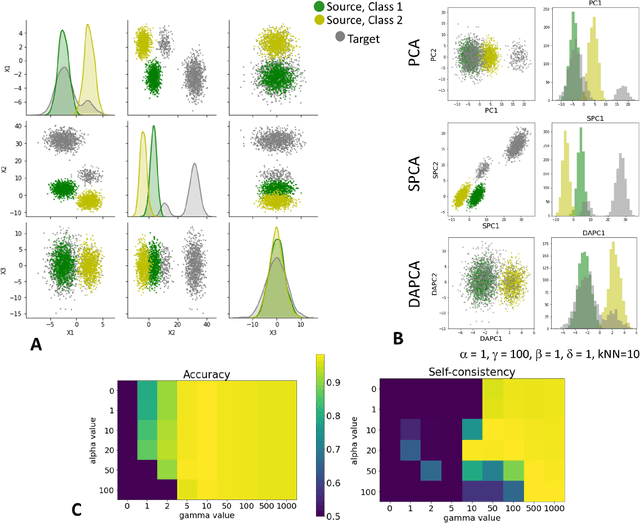
Domain adaptation is a popular paradigm in modern machine learning which aims at tackling the problem of divergence between training or validation dataset possessing labels for learning and testing a classifier (source domain) and a potentially large unlabeled dataset where the model is exploited (target domain). The task is to find such a common representation of both source and target datasets in which the source dataset is informative for training and such that the divergence between source and target would be minimized. Most popular solutions for domain adaptation are currently based on training neural networks that combine classification and adversarial learning modules, which are data hungry and usually difficult to train. We present a method called Domain Adaptation Principal Component Analysis (DAPCA) which finds a linear reduced data representation useful for solving the domain adaptation task. DAPCA is based on introducing positive and negative weights between pairs of data points and generalizes the supervised extension of principal component analysis. DAPCA represents an iterative algorithm such that at each iteration a simple quadratic optimization problem is solved. The convergence of the algorithm is guaranteed and the number of iterations is small in practice. We validate the suggested algorithm on previously proposed benchmarks for solving the domain adaptation task, and also show the benefit of using DAPCA in the analysis of single cell omics datasets in biomedical applications. Overall, DAPCA can serve as a useful preprocessing step in many machine learning applications leading to reduced dataset representations, taking into account possible divergence between source and target domains.

High-dimensional separability for one- and few-shot learning

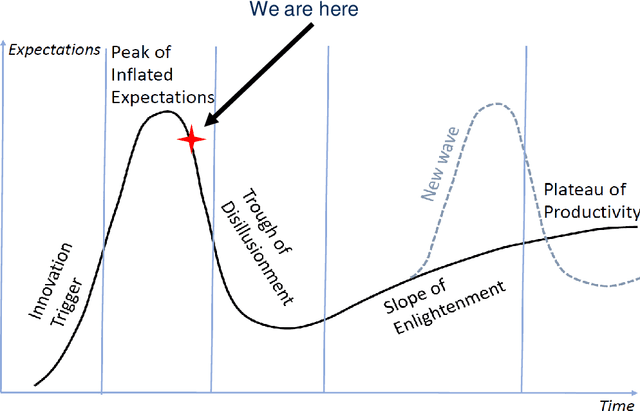
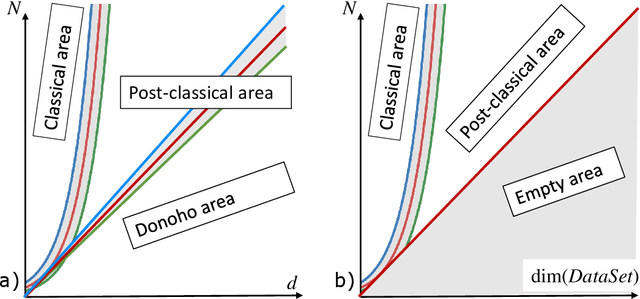
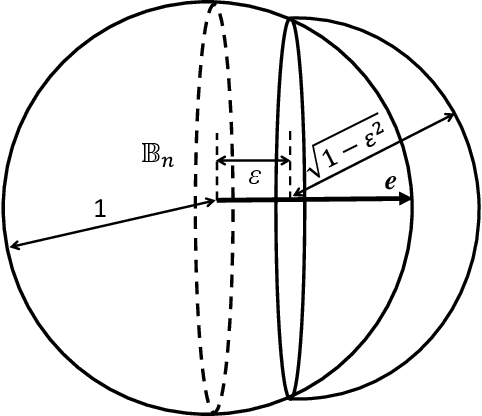
This work is driven by a practical question, corrections of Artificial Intelligence (AI) errors. Systematic re-training of a large AI system is hardly possible. To solve this problem, special external devices, correctors, are developed. They should provide quick and non-iterative system fix without modification of a legacy AI system. A common universal part of the AI corrector is a classifier that should separate undesired and erroneous behavior from normal operation. Training of such classifiers is a grand challenge at the heart of the one- and few-shot learning methods. Effectiveness of one- and few-short methods is based on either significant dimensionality reductions or the blessing of dimensionality effects. Stochastic separability is a blessing of dimensionality phenomenon that allows one-and few-shot error correction: in high-dimensional datasets under broad assumptions each point can be separated from the rest of the set by simple and robust linear discriminant. The hierarchical structure of data universe is introduced where each data cluster has a granular internal structure, etc. New stochastic separation theorems for the data distributions with fine-grained structure are formulated and proved. Separation theorems in infinite-dimensional limits are proven under assumptions of compact embedding of patterns into data space. New multi-correctors of AI systems are presented and illustrated with examples of predicting errors and learning new classes of objects by a deep convolutional neural network.