High-dimensional separability for one- and few-shot learning
Paper and Code
Jun 28, 2021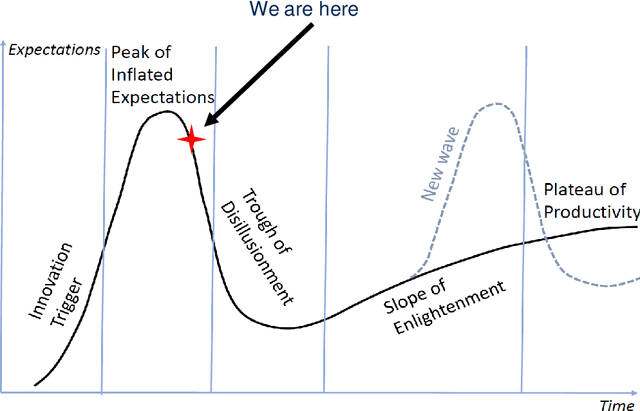

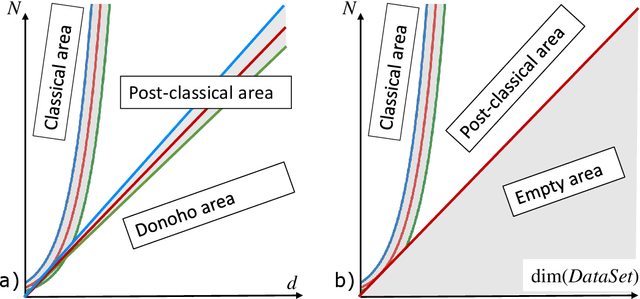
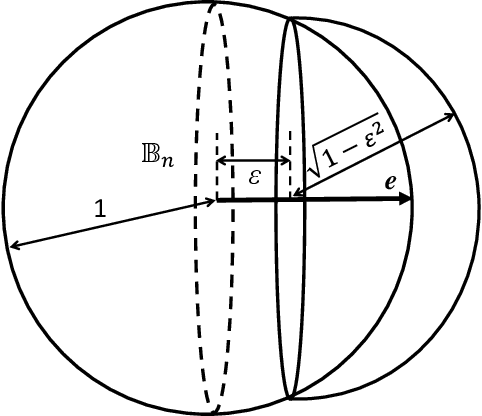
This work is driven by a practical question, corrections of Artificial Intelligence (AI) errors. Systematic re-training of a large AI system is hardly possible. To solve this problem, special external devices, correctors, are developed. They should provide quick and non-iterative system fix without modification of a legacy AI system. A common universal part of the AI corrector is a classifier that should separate undesired and erroneous behavior from normal operation. Training of such classifiers is a grand challenge at the heart of the one- and few-shot learning methods. Effectiveness of one- and few-short methods is based on either significant dimensionality reductions or the blessing of dimensionality effects. Stochastic separability is a blessing of dimensionality phenomenon that allows one-and few-shot error correction: in high-dimensional datasets under broad assumptions each point can be separated from the rest of the set by simple and robust linear discriminant. The hierarchical structure of data universe is introduced where each data cluster has a granular internal structure, etc. New stochastic separation theorems for the data distributions with fine-grained structure are formulated and proved. Separation theorems in infinite-dimensional limits are proven under assumptions of compact embedding of patterns into data space. New multi-correctors of AI systems are presented and illustrated with examples of predicting errors and learning new classes of objects by a deep convolutional neural network.
 Add to Chrome
Add to Chrome Add to Firefox
Add to Firefox Add to Edge
Add to Edge