Domain Adaptation Principal Component Analysis: base linear method for learning with out-of-distribution data

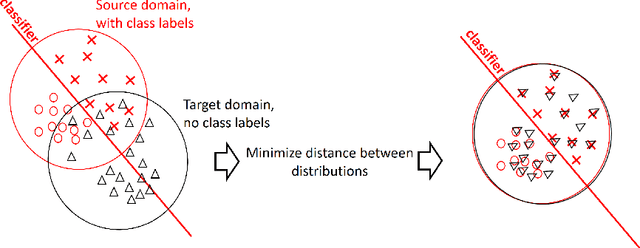
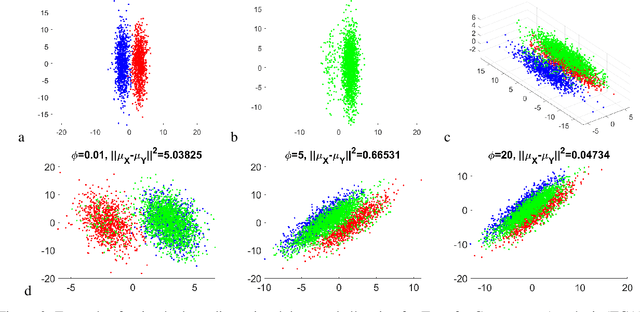
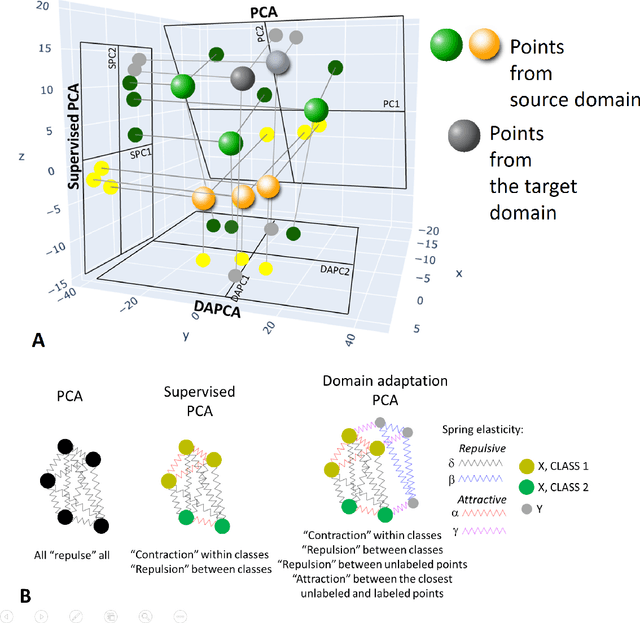
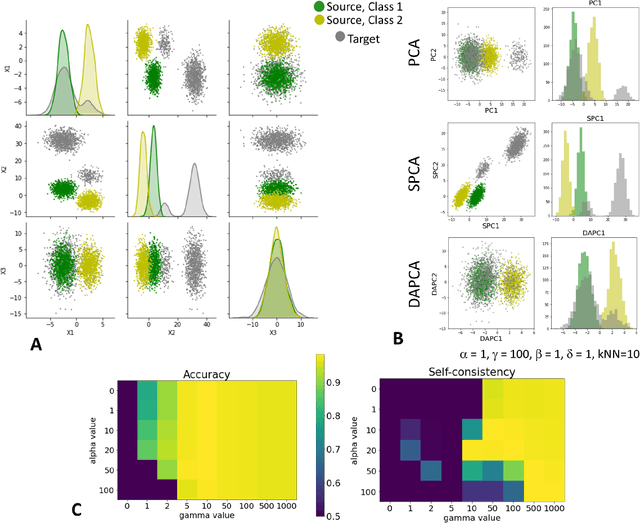
Domain adaptation is a popular paradigm in modern machine learning which aims at tackling the problem of divergence between training or validation dataset possessing labels for learning and testing a classifier (source domain) and a potentially large unlabeled dataset where the model is exploited (target domain). The task is to find such a common representation of both source and target datasets in which the source dataset is informative for training and such that the divergence between source and target would be minimized. Most popular solutions for domain adaptation are currently based on training neural networks that combine classification and adversarial learning modules, which are data hungry and usually difficult to train. We present a method called Domain Adaptation Principal Component Analysis (DAPCA) which finds a linear reduced data representation useful for solving the domain adaptation task. DAPCA is based on introducing positive and negative weights between pairs of data points and generalizes the supervised extension of principal component analysis. DAPCA represents an iterative algorithm such that at each iteration a simple quadratic optimization problem is solved. The convergence of the algorithm is guaranteed and the number of iterations is small in practice. We validate the suggested algorithm on previously proposed benchmarks for solving the domain adaptation task, and also show the benefit of using DAPCA in the analysis of single cell omics datasets in biomedical applications. Overall, DAPCA can serve as a useful preprocessing step in many machine learning applications leading to reduced dataset representations, taking into account possible divergence between source and target domains.

Artificial Neural Network Pruning to Extract Knowledge

Artificial Neural Networks (NN) are widely used for solving complex problems from medical diagnostics to face recognition. Despite notable successes, the main disadvantages of NN are also well known: the risk of overfitting, lack of explainability (inability to extract algorithms from trained NN), and high consumption of computing resources. Determining the appropriate specific NN structure for each problem can help overcome these difficulties: Too poor NN cannot be successfully trained, but too rich NN gives unexplainable results and may have a high chance of overfitting. Reducing precision of NN parameters simplifies the implementation of these NN, saves computing resources, and makes the NN skills more transparent. This paper lists the basic NN simplification problems and controlled pruning procedures to solve these problems. All the described pruning procedures can be implemented in one framework. The developed procedures, in particular, find the optimal structure of NN for each task, measure the influence of each input signal and NN parameter, and provide a detailed verbal description of the algorithms and skills of NN. The described methods are illustrated by a simple example: the generation of explicit algorithms for predicting the results of the US presidential election.