A Machine Learning Approach That Beats Large Rubik's Cubes

The paper proposes a novel machine learning-based approach to the pathfinding problem on extremely large graphs. This method leverages diffusion distance estimation via a neural network and uses beam search for pathfinding. We demonstrate its efficiency by finding solutions for 4x4x4 and 5x5x5 Rubik's cubes with unprecedentedly short solution lengths, outperforming all available solvers and introducing the first machine learning solver beyond the 3x3x3 case. In particular, it surpasses every single case of the combined best results in the Kaggle Santa 2023 challenge, which involved over 1,000 teams. For the 3x3x3 Rubik's cube, our approach achieves an optimality rate exceeding 98%, matching the performance of task-specific solvers and significantly outperforming prior solutions such as DeepCubeA (60.3%) and EfficientCube (69.6%). Additionally, our solution is more than 26 times faster in solving 3x3x3 Rubik's cubes while requiring up to 18.5 times less model training time than the most efficient state-of-the-art competitor.

Trajectories, bifurcations and pseudotime in large clinical datasets: applications to myocardial infarction and diabetes data

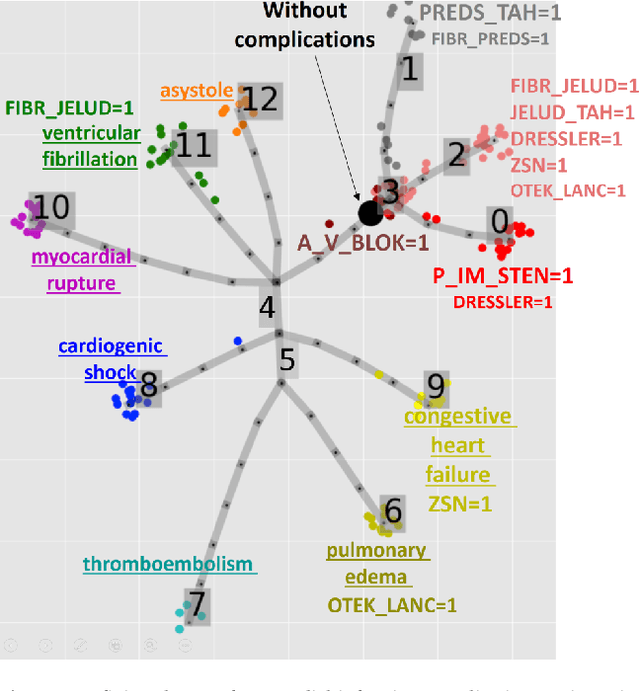
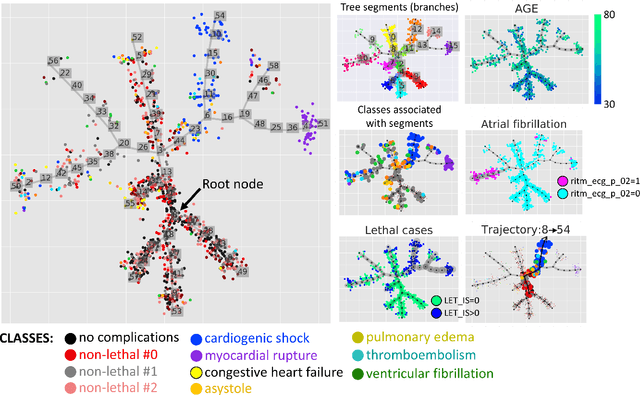
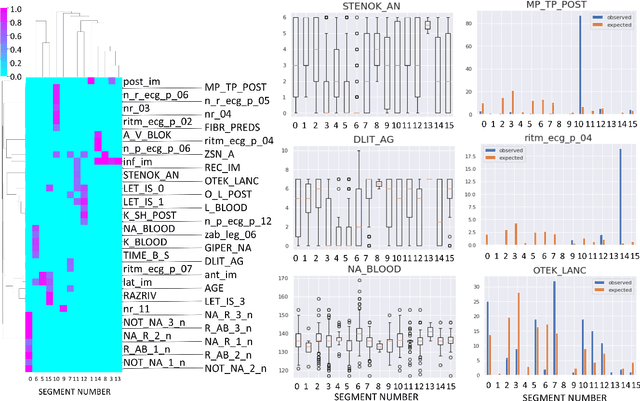
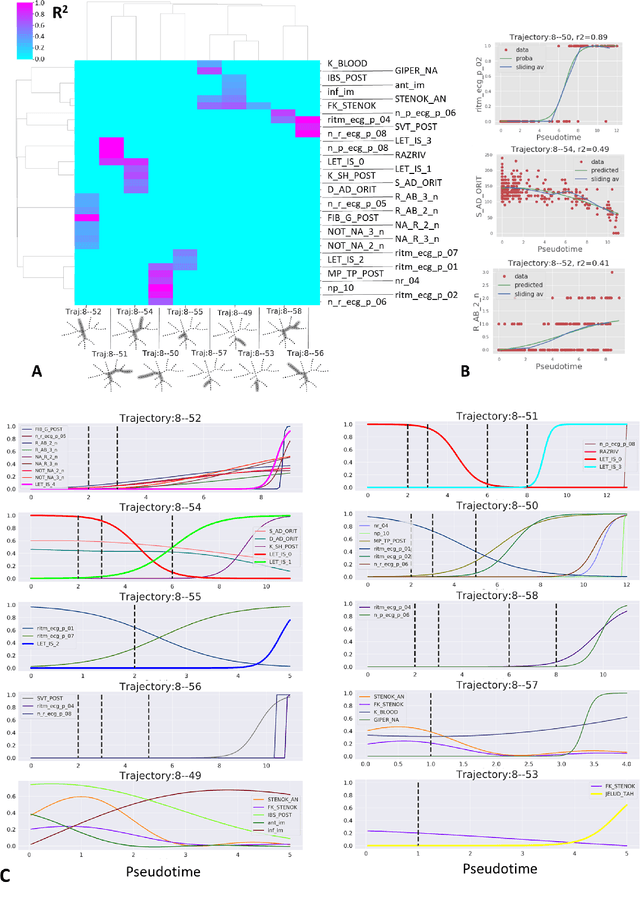
Large observational clinical datasets become increasingly available for mining associations between various disease traits and administered therapy. These datasets can be considered as representations of the landscape of all possible disease conditions, in which a concrete pathology develops through a number of stereotypical routes, characterized by `points of no return' and `final states' (such as lethal or recovery states). Extracting this information directly from the data remains challenging, especially in the case of synchronic (with a short-term follow up) observations. Here we suggest a semi-supervised methodology for the analysis of large clinical datasets, characterized by mixed data types and missing values, through modeling the geometrical data structure as a bouquet of bifurcating clinical trajectories. The methodology is based on application of elastic principal graphs which can address simultaneously the tasks of dimensionality reduction, data visualization, clustering, feature selection and quantifying the geodesic distances (pseudotime) in partially ordered sequences of observations. The methodology allows positioning a patient on a particular clinical trajectory (pathological scenario) and characterizing the degree of progression along it with a qualitative estimate of the uncertainty of the prognosis. Overall, our pseudo-time quantification-based approach gives a possibility to apply the methods developed for dynamical disease phenotyping and illness trajectory analysis (diachronic data analysis) to synchronic observational data. We developed a tool $ClinTrajan$ for clinical trajectory analysis implemented in Python programming language. We test the methodology in two large publicly available datasets: myocardial infarction complications and readmission of diabetic patients data.