Improving regional weather forecasts with neural interpolation

In this paper we design a neural interpolation operator to improve the boundary data for regional weather models, which is a challenging problem as we are required to map multi-scale dynamics between grid resolutions. In particular, we expose a methodology for approaching the problem through the study of a simplified model, with a view to generalise the results in this work to the dynamical core of regional weather models. Our approach will exploit a combination of techniques from image super-resolution with convolutional neural networks (CNNs) and residual networks, in addition to building the flow of atmospheric dynamics into the neural network

The Boundaries of Verifiable Accuracy, Robustness, and Generalisation in Deep Learning

In this work, we assess the theoretical limitations of determining guaranteed stability and accuracy of neural networks in classification tasks. We consider classical distribution-agnostic framework and algorithms minimising empirical risks and potentially subjected to some weights regularisation. We show that there is a large family of tasks for which computing and verifying ideal stable and accurate neural networks in the above settings is extremely challenging, if at all possible, even when such ideal solutions exist within the given class of neural architectures.

Learning from few examples with nonlinear feature maps

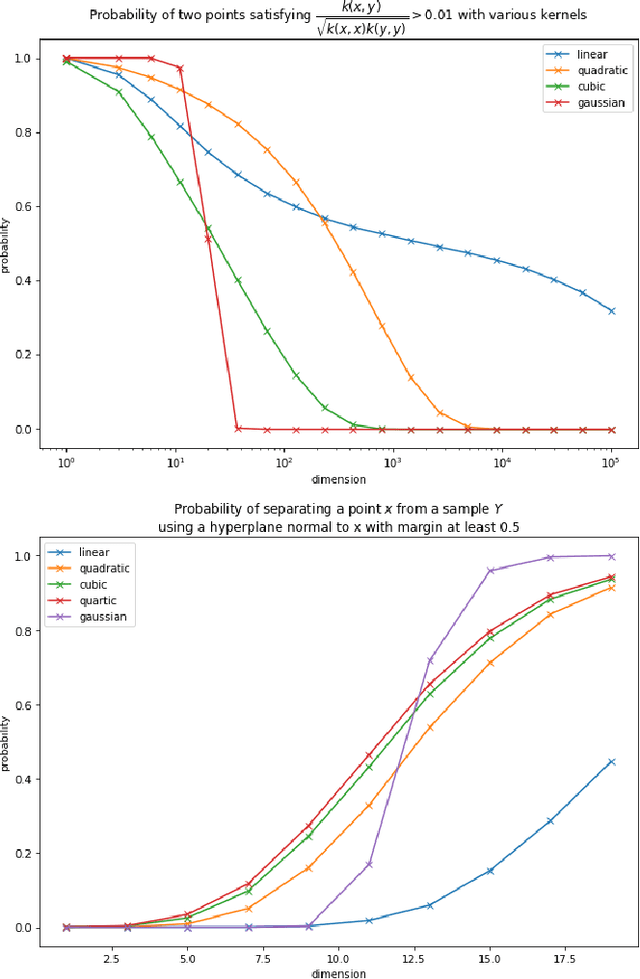
In this work we consider the problem of data classification in post-classical settings were the number of training examples consists of mere few data points. We explore the phenomenon and reveal key relationships between dimensionality of AI model's feature space, non-degeneracy of data distributions, and the model's generalisation capabilities. The main thrust of our present analysis is on the influence of nonlinear feature transformations mapping original data into higher- and possibly infinite-dimensional spaces on the resulting model's generalisation capabilities. Subject to appropriate assumptions, we establish new relationships between intrinsic dimensions of the transformed data and the probabilities to learn successfully from few presentations.