Complete Identification of Deep ReLU Neural Networks by Many-Valued Logic

Deep ReLU neural networks admit nontrivial functional symmetries: vastly different architectures and parameters (weights and biases) can realize the same function. We address the complete identification problem -- given a function f, deriving the architecture and parameters of all feedforward ReLU networks giving rise to f. We translate ReLU networks into Lukasiewicz logic formulae, and effect functional equivalent network transformations through algebraic rewrites governed by the logic axioms. A compositional norm form is proposed to facilitate the mapping from Lukasiewicz logic formulae back to ReLU networks. Using Chang's completeness theorem, we show that for every functional equivalence class, all ReLU networks in that class are connected by a finite set of symmetries corresponding to the finite set of axioms of Lukasiewicz logic. This idea is reminiscent of Shannon's seminal work on switching circuit design, where the circuits are translated into Boolean formulae, and synthesis is effected by algebraic rewriting governed by Boolean logic axioms.

Grounding Beyond Detection: Enhancing Contextual Understanding in Embodied 3D Grounding

Embodied 3D grounding aims to localize target objects described in human instructions from ego-centric viewpoint. Most methods typically follow a two-stage paradigm where a trained 3D detector's optimized backbone parameters are used to initialize a grounding model. In this study, we explore a fundamental question: Does embodied 3D grounding benefit enough from detection? To answer this question, we assess the grounding performance of detection models using predicted boxes filtered by the target category. Surprisingly, these detection models without any instruction-specific training outperform the grounding models explicitly trained with language instructions. This indicates that even category-level embodied 3D grounding may not be well resolved, let alone more fine-grained context-aware grounding. Motivated by this finding, we propose DEGround, which shares DETR queries as object representation for both DEtection and Grounding and enables the grounding to benefit from basic category classification and box detection. Based on this framework, we further introduce a regional activation grounding module that highlights instruction-related regions and a query-wise modulation module that incorporates sentence-level semantic into the query representation, strengthening the context-aware understanding of language instructions. Remarkably, DEGround outperforms state-of-the-art model BIP3D by 7.52\% at overall accuracy on the EmbodiedScan validation set. The source code will be publicly available at https://github.com/zyn213/DEGround.

Multi-Neuron Unleashes Expressivity of ReLU Networks Under Convex Relaxation

Neural work certification has established itself as a crucial tool for ensuring the robustness of neural networks. Certification methods typically rely on convex relaxations of the feasible output set to provide sound bounds. However, complete certification requires exact bounds, which strongly limits the expressivity of ReLU networks: even for the simple ``$\max$'' function in $\mathbb{R}^2$, there does not exist a ReLU network that expresses this function and can be exactly bounded by single-neuron relaxation methods. This raises the question whether there exists a convex relaxation that can provide exact bounds for general continuous piecewise linear functions in $\mathbb{R}^n$. In this work, we answer this question affirmatively by showing that (layer-wise) multi-neuron relaxation provides complete certification for general ReLU networks. Based on this novel result, we show that the expressivity of ReLU networks is no longer limited under multi-neuron relaxation. To the best of our knowledge, this is the first positive result on the completeness of convex relaxations, shedding light on the practice of certified robustness.

Bootstrapping Referring Multi-Object Tracking

Referring multi-object tracking (RMOT) aims at detecting and tracking multiple objects following human instruction represented by a natural language expression. Existing RMOT benchmarks are usually formulated through manual annotations, integrated with static regulations. This approach results in a dearth of notable diversity and a constrained scope of implementation. In this work, our key idea is to bootstrap the task of referring multi-object tracking by introducing discriminative language words as much as possible. In specific, we first develop Refer-KITTI into a large-scale dataset, named Refer-KITTI-V2. It starts with 2,719 manual annotations, addressing the issue of class imbalance and introducing more keywords to make it closer to real-world scenarios compared to Refer-KITTI. They are further expanded to a total of 9,758 annotations by prompting large language models, which create 617 different words, surpassing previous RMOT benchmarks. In addition, the end-to-end framework in RMOT is also bootstrapped by a simple yet elegant temporal advancement strategy, which achieves better performance than previous approaches. The source code and dataset is available at https://github.com/zyn213/TempRMOT.

Cellular automata, many-valued logic, and deep neural networks

We develop a theory characterizing the fundamental capability of deep neural networks to learn, from evolution traces, the logical rules governing the behavior of cellular automata (CA). This is accomplished by first establishing a novel connection between CA and Lukasiewicz propositional logic. While binary CA have been known for decades to essentially perform operations in Boolean logic, no such relationship exists for general CA. We demonstrate that many-valued (MV) logic, specifically Lukasiewicz propositional logic, constitutes a suitable language for characterizing general CA as logical machines. This is done by interpolating CA transition functions to continuous piecewise linear functions, which, by virtue of the McNaughton theorem, yield formulae in MV logic characterizing the CA. Recognizing that deep rectified linear unit (ReLU) networks realize continuous piecewise linear functions, it follows that these formulae are naturally extracted from CA evolution traces by deep ReLU networks. A corresponding algorithm together with a software implementation is provided. Finally, we show that the dynamical behavior of CA can be realized by recurrent neural networks.

Extracting Formulae in Many-Valued Logic from Deep Neural Networks

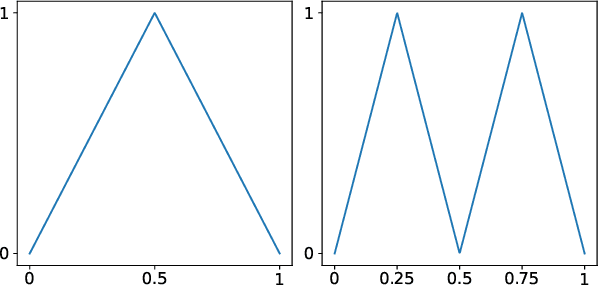
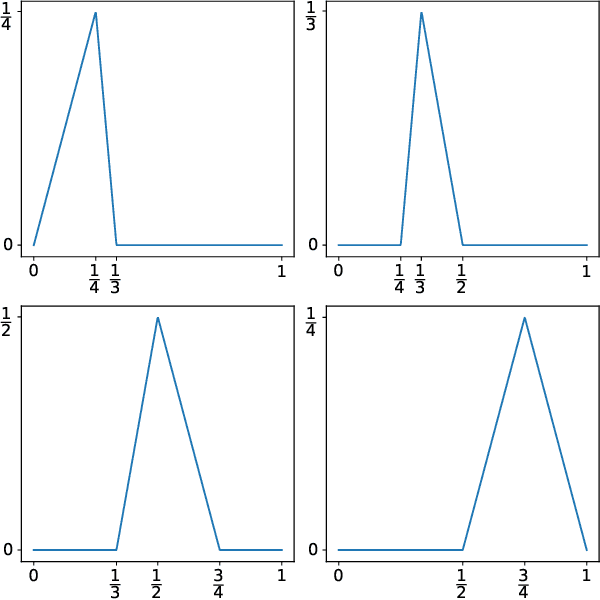
We propose a new perspective on deep ReLU networks, namely as circuit counterparts of Lukasiewicz infinite-valued logic -- a many-valued (MV) generalization of Boolean logic. An algorithm for extracting formulae in MV logic from deep ReLU networks is presented. As the algorithm applies to networks with general, in particular also real-valued, weights, it can be used to extract logical formulae from deep ReLU networks trained on data.