Convergent Dynamics for Solving the TAP Equations of Ising Models with Arbitrary Rotation Invariant Coupling Matrices

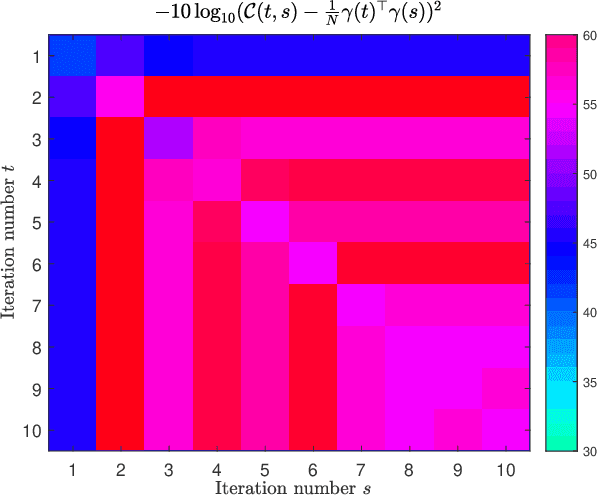
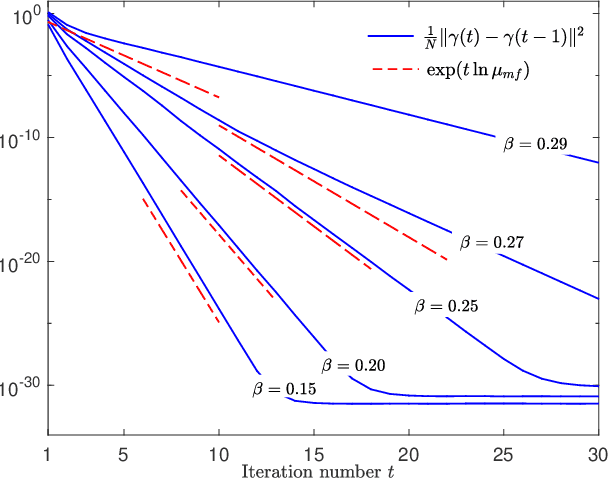
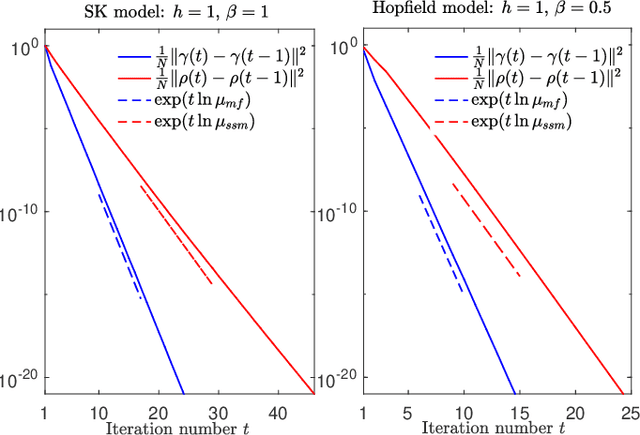
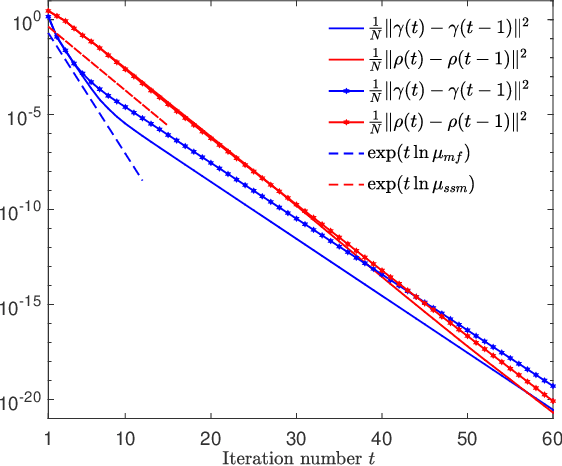
We propose an iterative algorithm for solving the Thouless-Anderson-Palmer (TAP) equations of Ising models with arbitrary rotation invariant (random) coupling matrices. In the large-system limit, as the number of iterations tends to infinity we prove by means of the dynamical functional method that the proposed algorithm converges when the so-called de Almeida Thouless (AT) criterion is fulfilled. Moreover, we obtain an analytical expression for the rate of the convergence.