Exact solution to the random sequential dynamics of a message passing algorithm
Paper and Code
Jan 05, 2021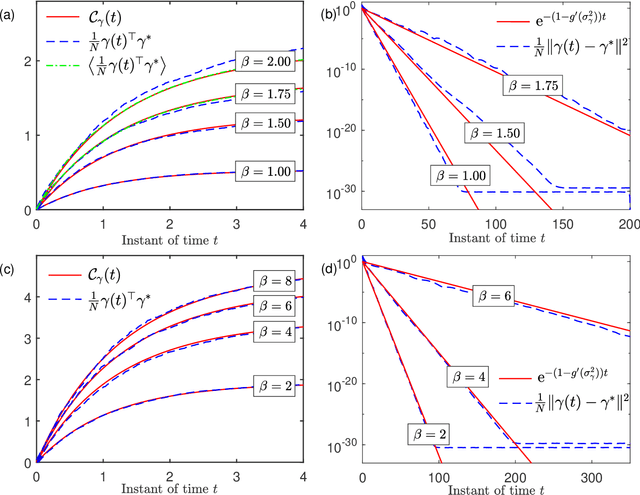
We analyze the random sequential dynamics of a message passing algorithm for Ising models with random interactions in the large system limit. We derive exact results for the two-time correlation functions and the speed of convergence. The {\em de Almedia-Thouless} stability criterion of the static problem is found to be necessary and sufficient for the global convergence of the random sequential dynamics.
* 5 pages
 Add to Chrome
Add to Chrome Add to Firefox
Add to Firefox Add to Edge
Add to Edge