Probability Distribution of Hypervolume Improvement in Bi-objective Bayesian Optimization
Paper and Code
May 12, 2022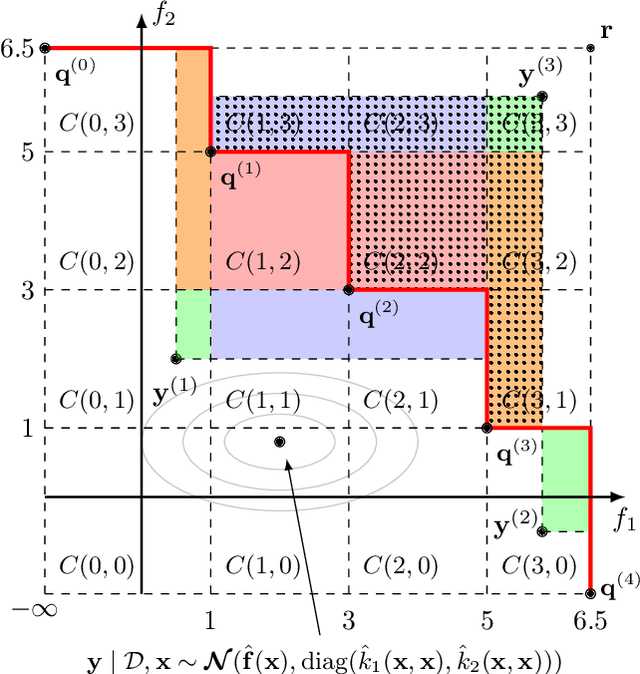

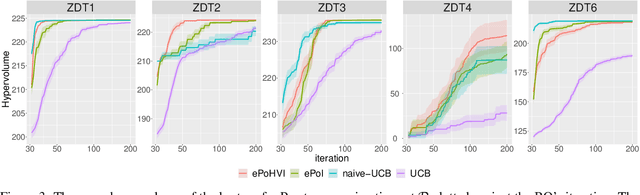

This work provides the exact expression of the probability distribution of the hypervolume improvement (HVI) for bi-objective generalization of Bayesian optimization. Here, instead of a single-objective improvement, we consider the improvement of the hypervolume indicator concerning the current best approximation of the Pareto front. Gaussian process regression models are trained independently on both objective functions, resulting in a bi-variate separated Gaussian distribution serving as a predictive model for the vector-valued objective function. Some commonly HVI-based acquisition functions (probability of improvement and upper confidence bound) are also leveraged with the help of the exact distribution of HVI. In addition, we show the superior numerical accuracy and efficiency of the exact distribution compared to the commonly used approximation by Monte-Carlo sampling. Finally, we benchmark distribution-leveraged acquisition functions on the widely applied ZDT problem set, demonstrating a significant advantage of using the exact distribution of HVI in multi-objective Bayesian optimization.
 Add to Chrome
Add to Chrome Add to Firefox
Add to Firefox Add to Edge
Add to Edge