Fast Mutation in Crossover-based Algorithms

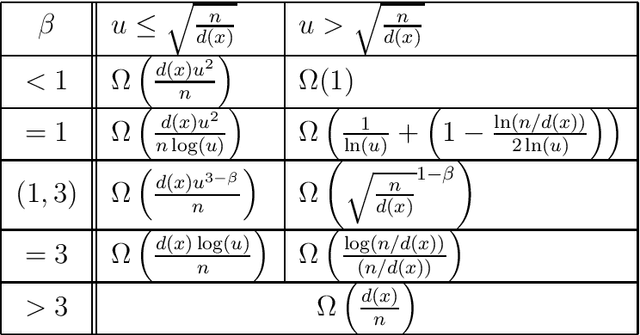
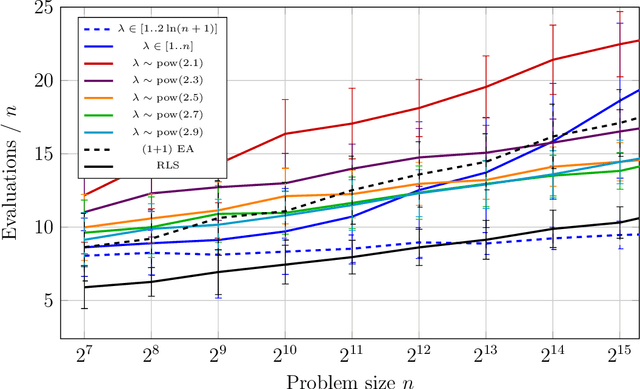
The heavy-tailed mutation operator proposed in Doerr et al. (GECCO 2017), called fast mutation to agree with the previously used language, so far was successfully used only in purely mutation-based algorithms. There, it can relieve the algorithm designer from finding the optimal mutation rate and nevertheless obtain a performance close to the one that the optimal mutation rate gives. In this first runtime analysis of a crossover-based algorithm using a heavy-tailed choice of the mutation rate, we show an even stronger impact. With a heavy-tailed mutation rate, the runtime of the $(1+(\lambda,\lambda))$ genetic algorithm on the OneMax benchmark function becomes linear in the problem size. This is asymptotically faster than with any static mutation rate and is the same asymptotic runtime that can be obtained with a self-adjusting choice of the mutation rate. This result is complemented by an empirical study which shows the effectiveness of the fast mutation also on random MAX-3SAT instances.