Improving Many-objective Evolutionary Algorithms by Means of Expanded Cone Orders

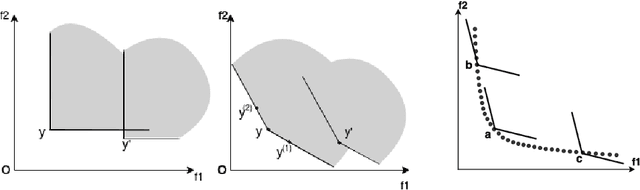
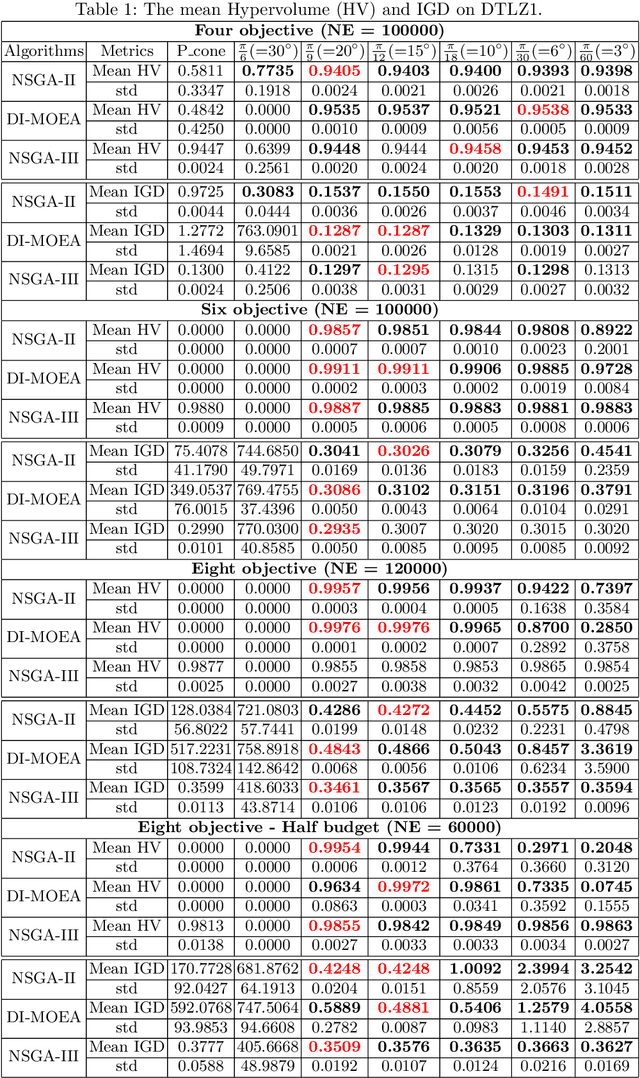
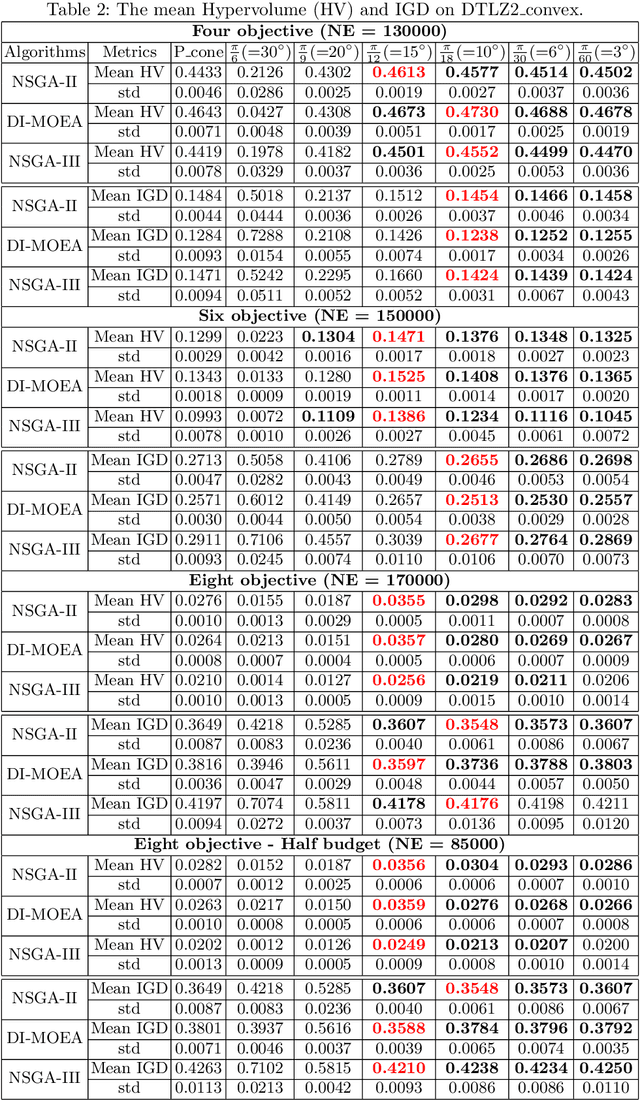
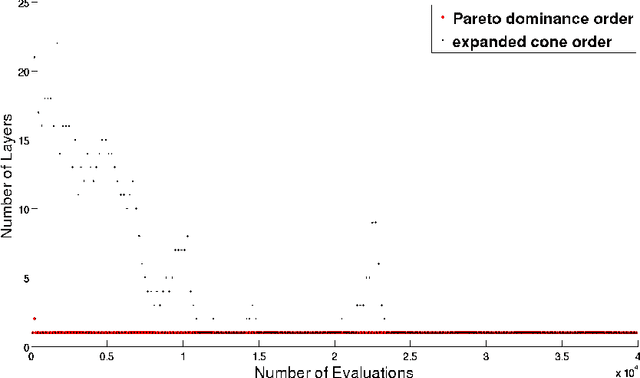
Given a point in m-dimensional objective space, the local environment of a point can be partitioned into the incomparable, the dominated and the dominating region. The ratio between the size of the incomparable region, and the dominated (and dominating) decreases proportionally to $1/2^{m-1}$. Due to this reason, it gets increasingly unlikely that dominating points can be found by random, isotropic mutations. As a remedy to stagnation of search in many objective optimization, in this paper, we suggest to enhance the Pareto dominance order by involving a convex obtuse dominance cone in the convergence phase of an evolutionary optimization algorithm. The approach is integrated in several state-of-the-art multi-objective evolutionary algorithms (MOEAs) and tested on benchmark problems with four, five, six and eight objectives. Computational experiments demonstrate the ability of the expanded cone technique to improve the performance of MOEAs on many-objective optimization problems.