Explainable Artificial Intelligence for Exhaust Gas Temperature of Turbofan Engines

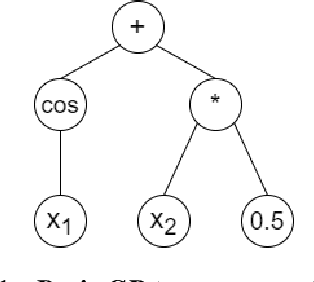
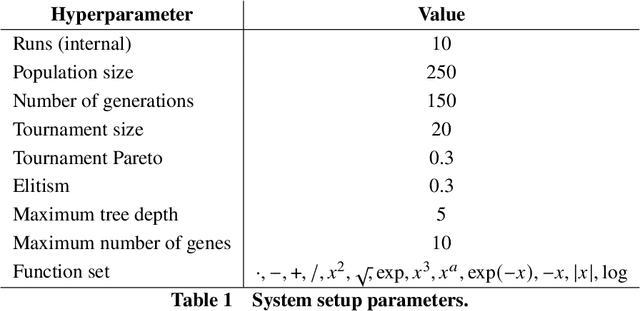
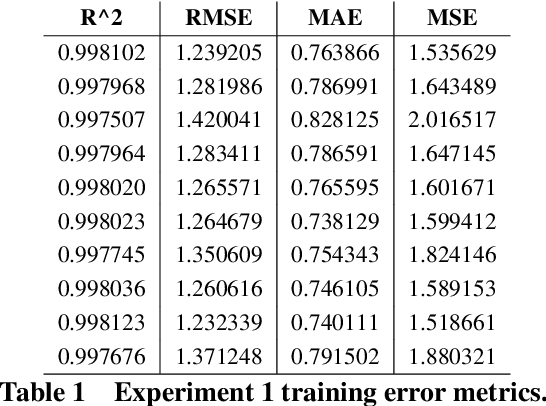
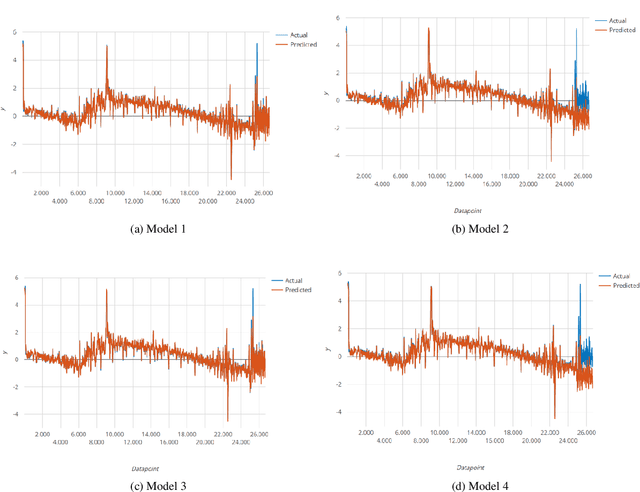
Data-driven modeling is an imperative tool in various industrial applications, including many applications in the sectors of aeronautics and commercial aviation. These models are in charge of providing key insights, such as which parameters are important on a specific measured outcome or which parameter values we should expect to observe given a set of input parameters. At the same time, however, these models rely heavily on assumptions (e.g., stationarity) or are "black box" (e.g., deep neural networks), meaning that they lack interpretability of their internal working and can be viewed only in terms of their inputs and outputs. An interpretable alternative to the "black box" models and with considerably less assumptions is symbolic regression (SR). SR searches for the optimal model structure while simultaneously optimizing the model's parameters without relying on an a-priori model structure. In this work, we apply SR on real-life exhaust gas temperature (EGT) data, collected at high frequencies through the entire flight, in order to uncover meaningful algebraic relationships between the EGT and other measurable engine parameters. The experimental results exhibit promising model accuracy, as well as explainability returning an absolute difference of 3{\deg}C compared to the ground truth and demonstrating consistency from an engineering perspective.

Multiple Node Immunisation for Preventing Epidemics on Networks by Exact Multiobjective Optimisation of Cost and Shield-Value

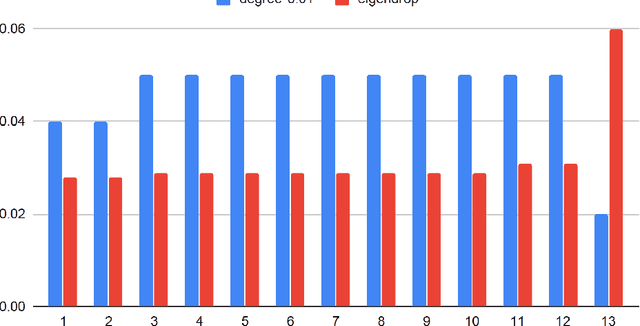
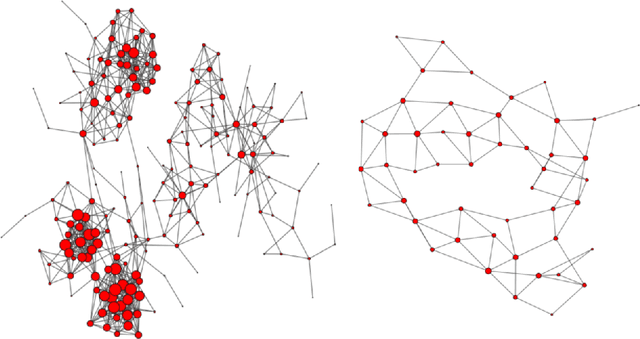
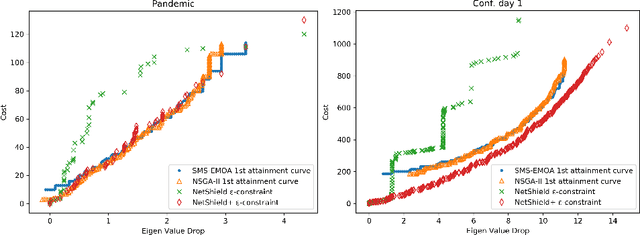
The general problem in this paper is vertex (node) subset selection with the goal to contain an infection that spreads in a network. Instead of selecting the single most important node, this paper deals with the problem of selecting multiple nodes for removal. As compared to previous work on multiple-node selection, the trade-off between cost and benefit is considered. The benefit is measured in terms of increasing the epidemic threshold which is a measure of how difficult it is for an infection to spread in a network. The cost is measured in terms of the number and size of nodes to be removed or controlled. Already in its single-objective instance with a fixed number of $k$ nodes to be removed, the multiple vertex immunisation problems have been proven to be NP-hard. Several heuristics have been developed to approximate the problem. In this work, we compare meta-heuristic techniques with exact methods on the Shield-value, which is a sub-modular proxy for the maximal eigenvalue and used in the current state-of-the-art greedy node-removal strategies. We generalise it to the multi-objective case and replace the greedy algorithm by a quadratic program (QP), which then can be solved with exact QP solvers. The main contribution of this paper is the insight that, if time permits, exact and problem-specific methods approximation should be used, which are often far better than Pareto front approximations obtained by general meta-heuristics. Based on these, it will be more effective to develop strategies for controlling real-world networks when the goal is to prevent or contain epidemic outbreaks. This paper is supported by ready to use Python implementation of the optimization methods and datasets.