$(ε, δ)$-Differentially Private Partial Least Squares Regression

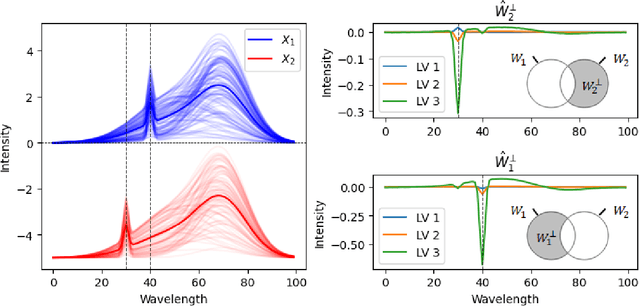
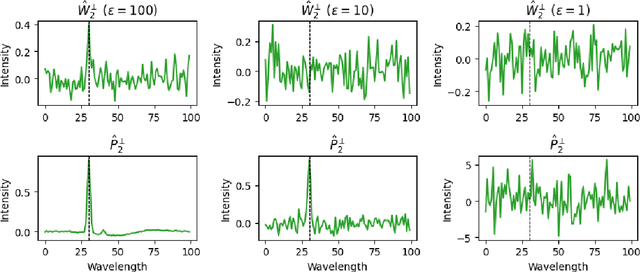
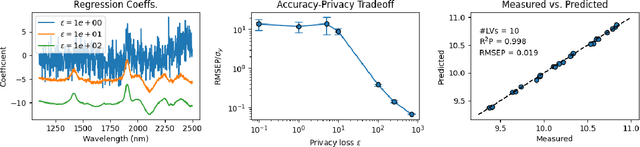
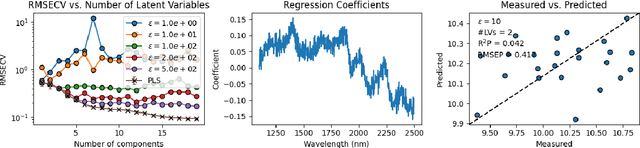
As data-privacy requirements are becoming increasingly stringent and statistical models based on sensitive data are being deployed and used more routinely, protecting data-privacy becomes pivotal. Partial Least Squares (PLS) regression is the premier tool for building such models in analytical chemistry, yet it does not inherently provide privacy guarantees, leaving sensitive (training) data vulnerable to privacy attacks. To address this gap, we propose an $(\epsilon, \delta)$-differentially private PLS (edPLS) algorithm, which integrates well-studied and theoretically motivated Gaussian noise-adding mechanisms into the PLS algorithm to ensure the privacy of the data underlying the model. Our approach involves adding carefully calibrated Gaussian noise to the outputs of four key functions in the PLS algorithm: the weights, scores, $X$-loadings, and $Y$-loadings. The noise variance is determined based on the global sensitivity of each function, ensuring that the privacy loss is controlled according to the $(\epsilon, \delta)$-differential privacy framework. Specifically, we derive the sensitivity bounds for each function and use these bounds to calibrate the noise added to the model components. Experimental results demonstrate that edPLS effectively renders privacy attacks, aimed at recovering unique sources of variability in the training data, ineffective. Application of edPLS to the NIR corn benchmark dataset shows that the root mean squared error of prediction (RMSEP) remains competitive even at strong privacy levels (i.e., $\epsilon=1$), given proper pre-processing of the corresponding spectra. These findings highlight the practical utility of edPLS in creating privacy-preserving multivariate calibrations and for the analysis of their privacy-utility trade-offs.

P3LS: Partial Least Squares under Privacy Preservation

Modern manufacturing value chains require intelligent orchestration of processes across company borders in order to maximize profits while fostering social and environmental sustainability. However, the implementation of integrated, systems-level approaches for data-informed decision-making along value chains is currently hampered by privacy concerns associated with cross-organizational data exchange and integration. We here propose Privacy-Preserving Partial Least Squares (P3LS) regression, a novel federated learning technique that enables cross-organizational data integration and process modeling with privacy guarantees. P3LS involves a singular value decomposition (SVD) based PLS algorithm and employs removable, random masks generated by a trusted authority in order to protect the privacy of the data contributed by each data holder. We demonstrate the capability of P3LS to vertically integrate process data along a hypothetical value chain consisting of three parties and to improve the prediction performance on several process-related key performance indicators. Furthermore, we show the numerical equivalence of P3LS and PLS model components on simulated data and provide a thorough privacy analysis of the former. Moreover, we propose a mechanism for determining the relevance of the contributed data to the problem being addressed, thus creating a basis for quantifying the contribution of participants.

Towards Vertical Privacy-Preserving Symbolic Regression via Secure Multiparty Computation

Symbolic Regression is a powerful data-driven technique that searches for mathematical expressions that explain the relationship between input variables and a target of interest. Due to its efficiency and flexibility, Genetic Programming can be seen as the standard search technique for Symbolic Regression. However, the conventional Genetic Programming algorithm requires storing all data in a central location, which is not always feasible due to growing concerns about data privacy and security. While privacy-preserving research has advanced recently and might offer a solution to this problem, their application to Symbolic Regression remains largely unexplored. Furthermore, the existing work only focuses on the horizontally partitioned setting, whereas the vertically partitioned setting, another popular scenario, has yet to be investigated. Herein, we propose an approach that employs a privacy-preserving technique called Secure Multiparty Computation to enable parties to jointly build Symbolic Regression models in the vertical scenario without revealing private data. Preliminary experimental results indicate that our proposed method delivers comparable performance to the centralized solution while safeguarding data privacy.

Towards federated multivariate statistical process control (FedMSPC)

The ongoing transition from a linear (produce-use-dispose) to a circular economy poses significant challenges to current state-of-the-art information and communication technologies. In particular, the derivation of integrated, high-level views on material, process, and product streams from (real-time) data produced along value chains is challenging for several reasons. Most importantly, sufficiently rich data is often available yet not shared across company borders because of privacy concerns which make it impossible to build integrated process models that capture the interrelations between input materials, process parameters, and key performance indicators along value chains. In the current contribution, we propose a privacy-preserving, federated multivariate statistical process control (FedMSPC) framework based on Federated Principal Component Analysis (PCA) and Secure Multiparty Computation to foster the incentive for closer collaboration of stakeholders along value chains. We tested our approach on two industrial benchmark data sets - SECOM and ST-AWFD. Our empirical results demonstrate the superior fault detection capability of the proposed approach compared to standard, single-party (multiway) PCA. Furthermore, we showcase the possibility of our framework to provide privacy-preserving fault diagnosis to each data holder in the value chain to underpin the benefits of secure data sharing and federated process modeling.