$(ε, δ)$-Differentially Private Partial Least Squares Regression

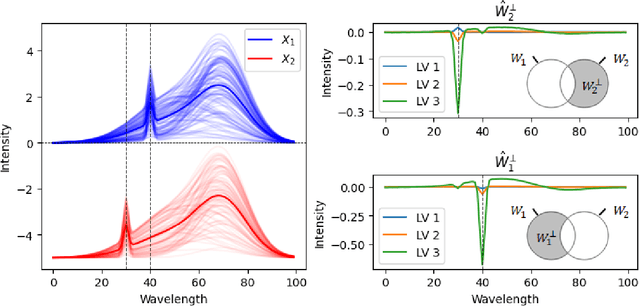
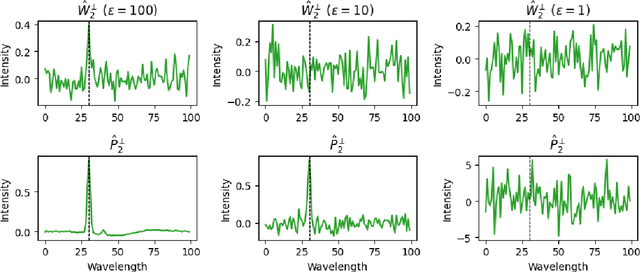
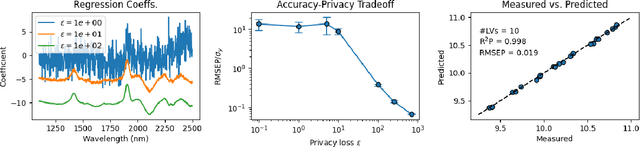
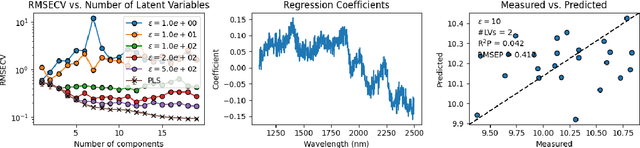
As data-privacy requirements are becoming increasingly stringent and statistical models based on sensitive data are being deployed and used more routinely, protecting data-privacy becomes pivotal. Partial Least Squares (PLS) regression is the premier tool for building such models in analytical chemistry, yet it does not inherently provide privacy guarantees, leaving sensitive (training) data vulnerable to privacy attacks. To address this gap, we propose an $(\epsilon, \delta)$-differentially private PLS (edPLS) algorithm, which integrates well-studied and theoretically motivated Gaussian noise-adding mechanisms into the PLS algorithm to ensure the privacy of the data underlying the model. Our approach involves adding carefully calibrated Gaussian noise to the outputs of four key functions in the PLS algorithm: the weights, scores, $X$-loadings, and $Y$-loadings. The noise variance is determined based on the global sensitivity of each function, ensuring that the privacy loss is controlled according to the $(\epsilon, \delta)$-differential privacy framework. Specifically, we derive the sensitivity bounds for each function and use these bounds to calibrate the noise added to the model components. Experimental results demonstrate that edPLS effectively renders privacy attacks, aimed at recovering unique sources of variability in the training data, ineffective. Application of edPLS to the NIR corn benchmark dataset shows that the root mean squared error of prediction (RMSEP) remains competitive even at strong privacy levels (i.e., $\epsilon=1$), given proper pre-processing of the corresponding spectra. These findings highlight the practical utility of edPLS in creating privacy-preserving multivariate calibrations and for the analysis of their privacy-utility trade-offs.

P3LS: Partial Least Squares under Privacy Preservation

Modern manufacturing value chains require intelligent orchestration of processes across company borders in order to maximize profits while fostering social and environmental sustainability. However, the implementation of integrated, systems-level approaches for data-informed decision-making along value chains is currently hampered by privacy concerns associated with cross-organizational data exchange and integration. We here propose Privacy-Preserving Partial Least Squares (P3LS) regression, a novel federated learning technique that enables cross-organizational data integration and process modeling with privacy guarantees. P3LS involves a singular value decomposition (SVD) based PLS algorithm and employs removable, random masks generated by a trusted authority in order to protect the privacy of the data contributed by each data holder. We demonstrate the capability of P3LS to vertically integrate process data along a hypothetical value chain consisting of three parties and to improve the prediction performance on several process-related key performance indicators. Furthermore, we show the numerical equivalence of P3LS and PLS model components on simulated data and provide a thorough privacy analysis of the former. Moreover, we propose a mechanism for determining the relevance of the contributed data to the problem being addressed, thus creating a basis for quantifying the contribution of participants.

Supervised and Penalized Baseline Correction

Spectroscopic measurements can show distorted spectra shapes arising from a mixture of absorbing and scattering contributions. These distortions (or baselines) often manifest themselves as non-constant offsets or low-frequency oscillations. As a result, these baselines can adversely affect analytical and quantitative results. Baseline correction is an umbrella term where one applies pre-processing methods to obtain baseline spectra (the unwanted distortions) and then remove the distortions by differencing. However, current state-of-the art baseline correction methods do not utilize analyte concentrations even if they are available, or even if they contribute significantly to the observed spectral variability. We examine a class of state-of-the-art methods (penalized baseline correction) and modify them such that they can accommodate a priori analyte concentration such that prediction can be enhanced. Performance will be access on two near infra-red data sets across both classical penalized baseline correction methods (without analyte information) and modified penalized baseline correction methods (leveraging analyte information).

Towards federated multivariate statistical process control (FedMSPC)

The ongoing transition from a linear (produce-use-dispose) to a circular economy poses significant challenges to current state-of-the-art information and communication technologies. In particular, the derivation of integrated, high-level views on material, process, and product streams from (real-time) data produced along value chains is challenging for several reasons. Most importantly, sufficiently rich data is often available yet not shared across company borders because of privacy concerns which make it impossible to build integrated process models that capture the interrelations between input materials, process parameters, and key performance indicators along value chains. In the current contribution, we propose a privacy-preserving, federated multivariate statistical process control (FedMSPC) framework based on Federated Principal Component Analysis (PCA) and Secure Multiparty Computation to foster the incentive for closer collaboration of stakeholders along value chains. We tested our approach on two industrial benchmark data sets - SECOM and ST-AWFD. Our empirical results demonstrate the superior fault detection capability of the proposed approach compared to standard, single-party (multiway) PCA. Furthermore, we showcase the possibility of our framework to provide privacy-preserving fault diagnosis to each data holder in the value chain to underpin the benefits of secure data sharing and federated process modeling.

Opening the black-box of Neighbor Embedding with Hotelling's T2 statistic and Q-residuals

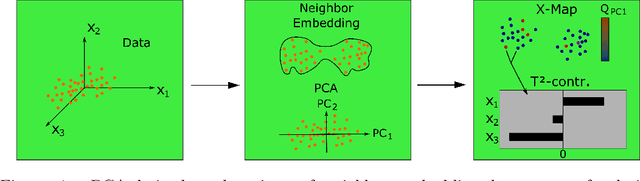
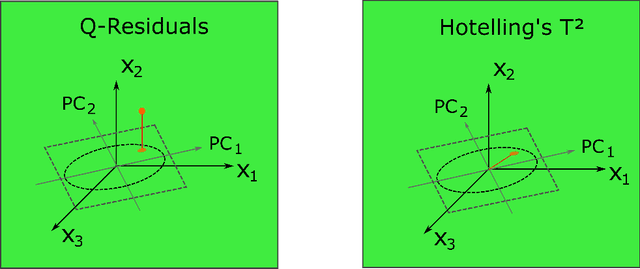
In contrast to classical techniques for exploratory analysis of high-dimensional data sets, such as principal component analysis (PCA), neighbor embedding (NE) techniques tend to better preserve the local structure/topology of high-dimensional data. However, the ability to preserve local structure comes at the expense of interpretability: Techniques such as t-Distributed Stochastic Neighbor Embedding (t-SNE) or Uniform Manifold Approximation and Projection (UMAP) do not give insights into which input variables underlie the topological (cluster) structure seen in the corresponding embedding. We here propose different "tricks" from the chemometrics field based on PCA, Q-residuals and Hotelling's T2 contributions in combination with novel visualization approaches to derive local and global explanations of neighbor embedding. We show how our approach is capable of identifying discriminatory features between groups of data points that remain unnoticed when exploring NEs using standard univariate or multivariate approaches.

Graph-based calibration transfer

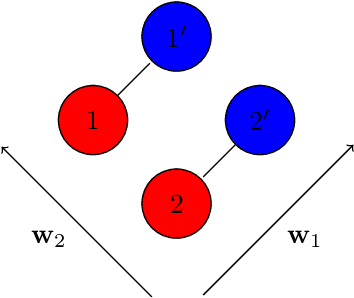
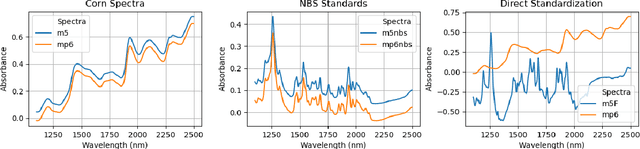
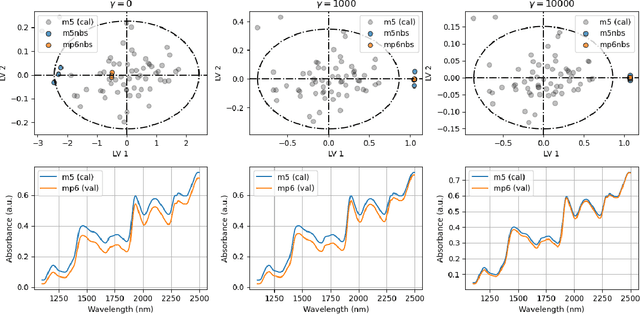
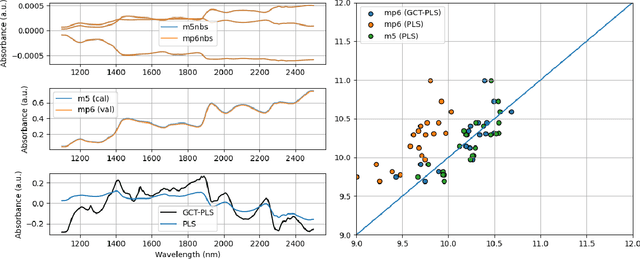
The problem of transferring calibrations from a primary to a secondary instrument, i.e. calibration transfer (CT), has been a matter of considerable research in chemometrics over the past decades. Current state-of-the-art (SoA) methods like (piecewise) direct standardization perform well when suitable transfer standards are available. However, stable calibration standards that share similar (spectral) features with the calibration samples are not always available. Towards enabling CT with arbitrary calibration standards, we propose a novel CT technique that employs manifold regularization of the partial least squares (PLS) objective. In particular, our method enforces that calibration standards, measured on primary and secondary instruments, have (nearly) invariant projections in the latent variable space of the primary calibration model. Thereby, our approach implicitly removes inter-device variation in the predictive directions of X which is in contrast to most state-of-the-art techniques that employ explicit pre-processing of the input data. We test our approach on the well-known corn benchmark data set employing the NBS glass standard spectra for instrument standardization and compare the results with current SoA methods.