Opening the black-box of Neighbor Embedding with Hotelling's T2 statistic and Q-residuals
Paper and Code
Sep 05, 2022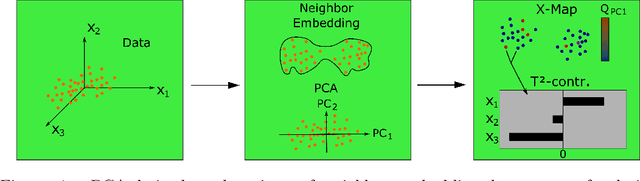
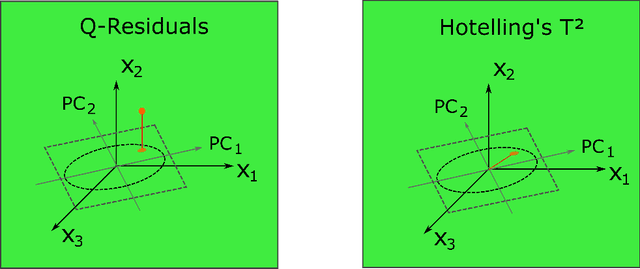
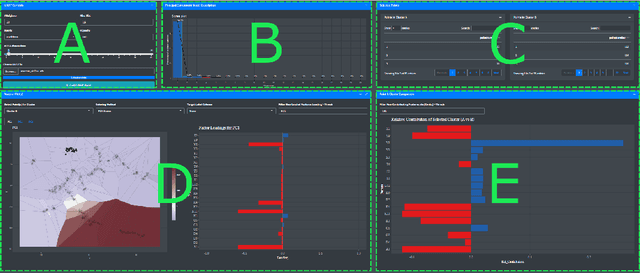
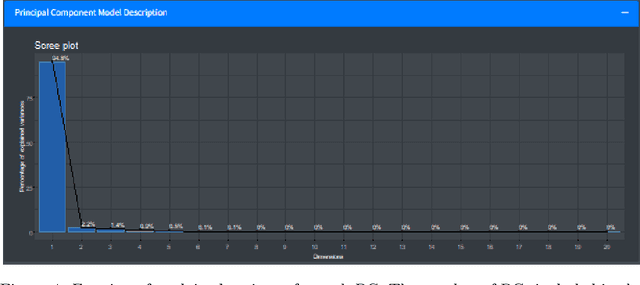
In contrast to classical techniques for exploratory analysis of high-dimensional data sets, such as principal component analysis (PCA), neighbor embedding (NE) techniques tend to better preserve the local structure/topology of high-dimensional data. However, the ability to preserve local structure comes at the expense of interpretability: Techniques such as t-Distributed Stochastic Neighbor Embedding (t-SNE) or Uniform Manifold Approximation and Projection (UMAP) do not give insights into which input variables underlie the topological (cluster) structure seen in the corresponding embedding. We here propose different "tricks" from the chemometrics field based on PCA, Q-residuals and Hotelling's T2 contributions in combination with novel visualization approaches to derive local and global explanations of neighbor embedding. We show how our approach is capable of identifying discriminatory features between groups of data points that remain unnoticed when exploring NEs using standard univariate or multivariate approaches.
 Add to Chrome
Add to Chrome Add to Firefox
Add to Firefox Add to Edge
Add to Edge