Hybrid Summary Statistics

We present a way to capture high-information posteriors from training sets that are sparsely sampled over the parameter space for robust simulation-based inference. In physical inference problems, we can often apply domain knowledge to define traditional summary statistics to capture some of the information in a dataset. We show that augmenting these statistics with neural network outputs to maximise the mutual information improves information extraction compared to neural summaries alone or their concatenation to existing summaries and makes inference robust in settings with low training data. We introduce 1) two loss formalisms to achieve this and 2) apply the technique to two different cosmological datasets to extract non-Gaussian parameter information.

Hybrid summary statistics: neural weak lensing inference beyond the power spectrum

In inference problems, we often have domain knowledge which allows us to define summary statistics that capture most of the information content in a dataset. In this paper, we present a hybrid approach, where such physics-based summaries are augmented by a set of compressed neural summary statistics that are optimised to extract the extra information that is not captured by the predefined summaries. The resulting statistics are very powerful inputs to simulation-based or implicit inference of model parameters. We apply this generalisation of Information Maximising Neural Networks (IMNNs) to parameter constraints from tomographic weak gravitational lensing convergence maps to find summary statistics that are explicitly optimised to complement angular power spectrum estimates. We study several dark matter simulation resolutions in low- and high-noise regimes. We show that i) the information-update formalism extracts at least $3\times$ and up to $8\times$ as much information as the angular power spectrum in all noise regimes, ii) the network summaries are highly complementary to existing 2-point summaries, and iii) our formalism allows for networks with smaller, physically-informed architectures to match much larger regression networks with far fewer simulations needed to obtain asymptotically optimal inference.

The Cosmic Graph: Optimal Information Extraction from Large-Scale Structure using Catalogues

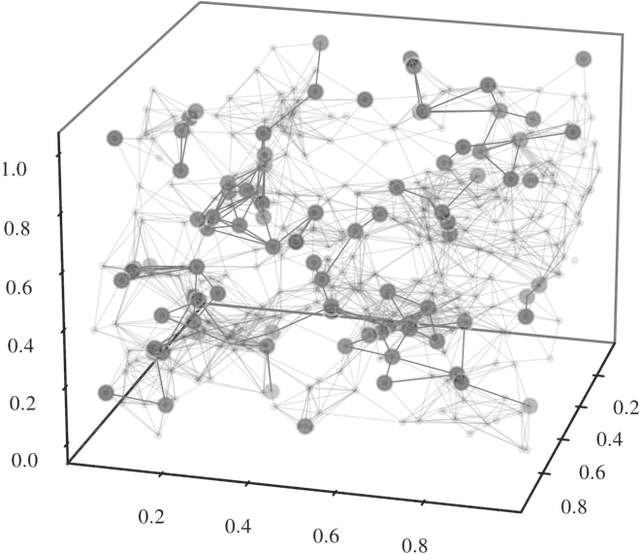
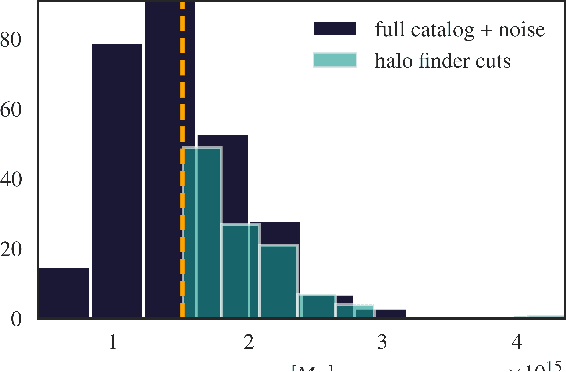
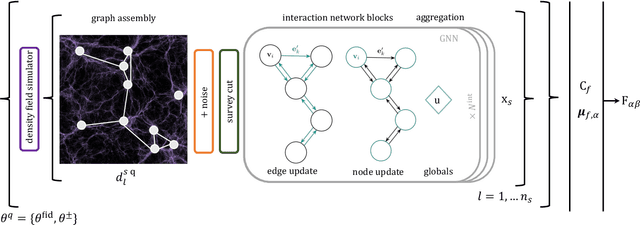
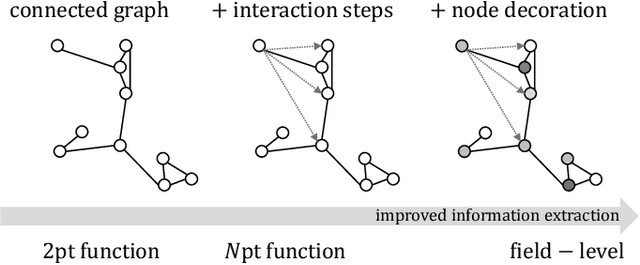
We present an implicit likelihood approach to quantifying cosmological information over discrete catalogue data, assembled as graphs. To do so, we explore cosmological inference using mock dark matter halo catalogues. We employ Information Maximising Neural Networks (IMNNs) to quantify Fisher information extraction as a function of graph representation. We a) demonstrate the high sensitivity of modular graph structure to the underlying cosmology in the noise-free limit, b) show that networks automatically combine mass and clustering information through comparisons to traditional statistics, c) demonstrate that graph neural networks can still extract information when catalogues are subject to noisy survey cuts, and d) illustrate how nonlinear IMNN summaries can be used as asymptotically optimal compressed statistics for Bayesian implicit likelihood inference. We reduce the area of joint $\Omega_m, \sigma_8$ parameter constraints with small ($\sim$100 object) halo catalogues by a factor of 42 over the two-point correlation function, and demonstrate that the networks automatically combine mass and clustering information. This work utilises a new IMNN implementation over graph data in Jax, which can take advantage of either numerical or auto-differentiability. We also show that graph IMNNs successfully compress simulations far from the fiducial model at which the network is fitted, indicating a promising alternative to $n$-point statistics in catalogue-based analyses.