Stephen Feeney
Fast likelihood-free cosmology with neural density estimators and active learning
Feb 28, 2019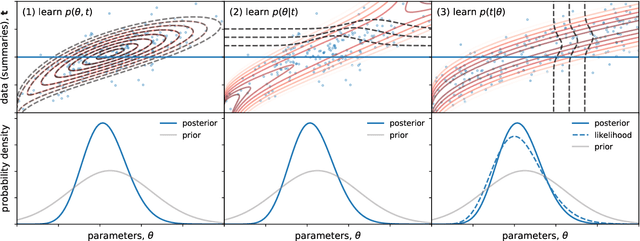
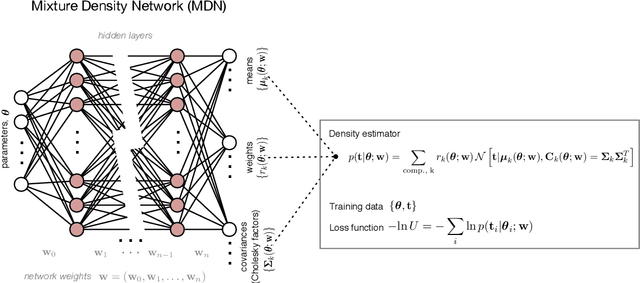
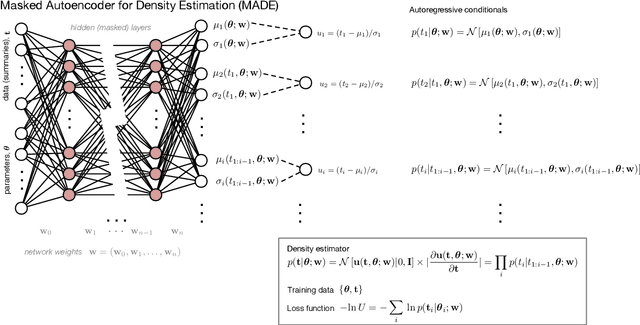
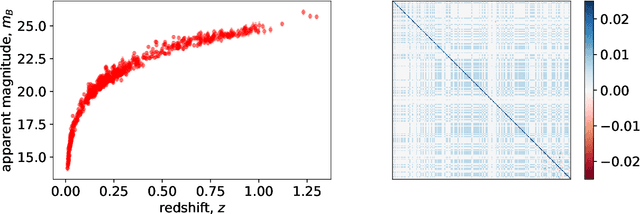
Abstract:Likelihood-free inference provides a framework for performing rigorous Bayesian inference using only forward simulations, properly accounting for all physical and observational effects that can be successfully included in the simulations. The key challenge for likelihood-free applications in cosmology, where simulation is typically expensive, is developing methods that can achieve high-fidelity posterior inference with as few simulations as possible. Density-estimation likelihood-free inference (DELFI) methods turn inference into a density estimation task on a set of simulated data-parameter pairs, and give orders of magnitude improvements over traditional Approximate Bayesian Computation approaches to likelihood-free inference. In this paper we use neural density estimators (NDEs) to learn the likelihood function from a set of simulated datasets, with active learning to adaptively acquire simulations in the most relevant regions of parameter space on-the-fly. We demonstrate the approach on a number of cosmological case studies, showing that for typical problems high-fidelity posterior inference can be achieved with just $\mathcal{O}(10^3)$ simulations or fewer. In addition to enabling efficient simulation-based inference, for simple problems where the form of the likelihood is known, DELFI offers a fast alternative to MCMC sampling, giving orders of magnitude speed-up in some cases. Finally, we introduce \textsc{pydelfi} -- a flexible public implementation of DELFI with NDEs and active learning -- available at \url{https://github.com/justinalsing/pydelfi}.
 Add to Chrome
Add to Chrome Add to Firefox
Add to Firefox Add to Edge
Add to Edge