Nested sampling with any prior you like
Paper and Code
Mar 09, 2021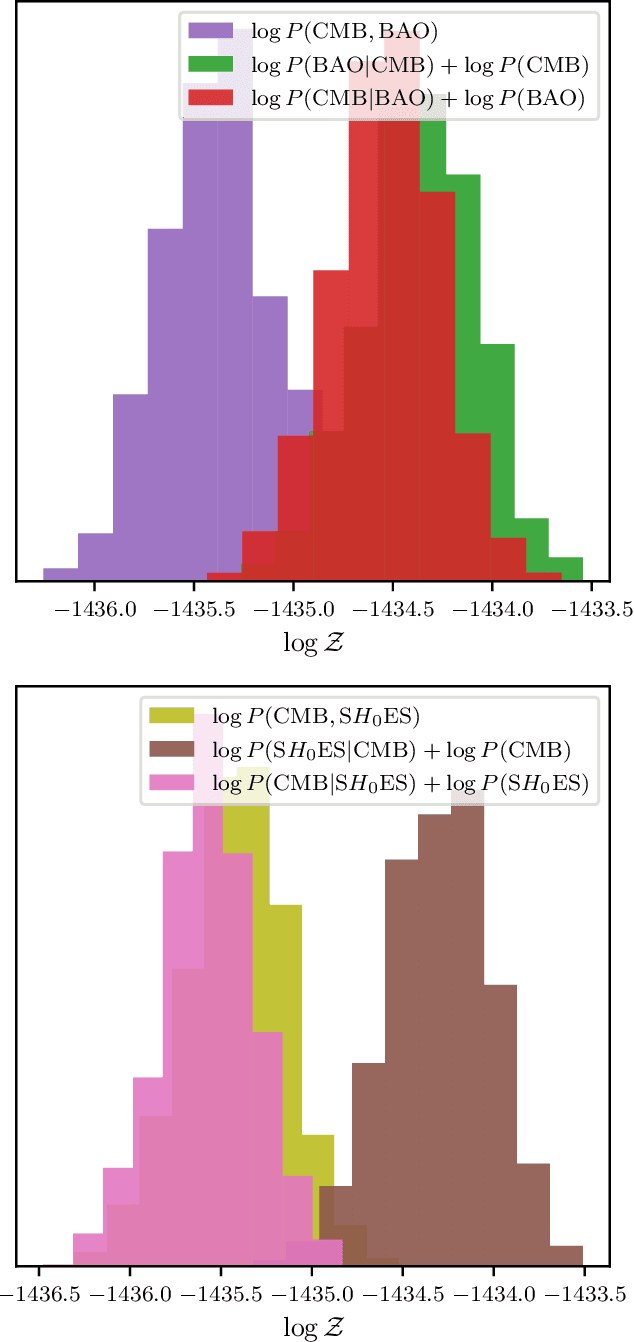
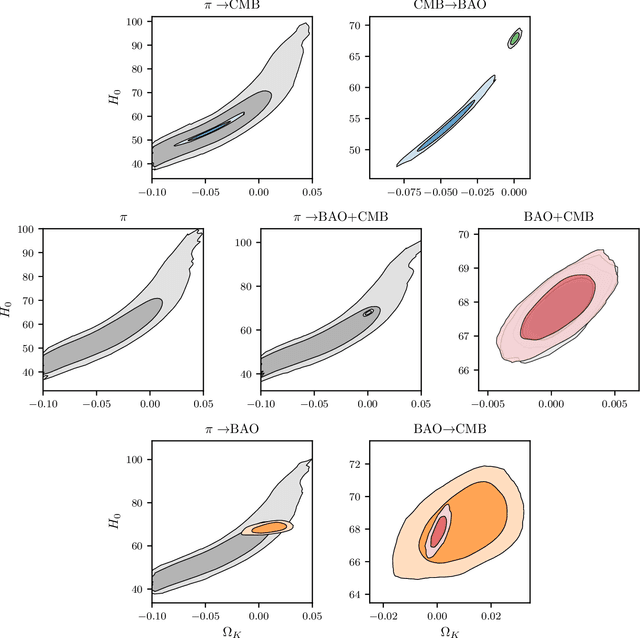
Nested sampling is an important tool for conducting Bayesian analysis in Astronomy and other fields, both for sampling complicated posterior distributions for parameter inference, and for computing marginal likelihoods for model comparison. One technical obstacle to using nested sampling in practice is the requirement (for most common implementations) that prior distributions be provided in the form of transformations from the unit hyper-cube to the target prior density. For many applications - particularly when using the posterior from one experiment as the prior for another - such a transformation is not readily available. In this letter we show that parametric bijectors trained on samples from a desired prior density provide a general-purpose method for constructing transformations from the uniform base density to a target prior, enabling the practical use of nested sampling under arbitrary priors. We demonstrate the use of trained bijectors in conjunction with nested sampling on a number of examples from cosmology.
 Add to Chrome
Add to Chrome Add to Firefox
Add to Firefox Add to Edge
Add to Edge