Graph Attention Retrospective

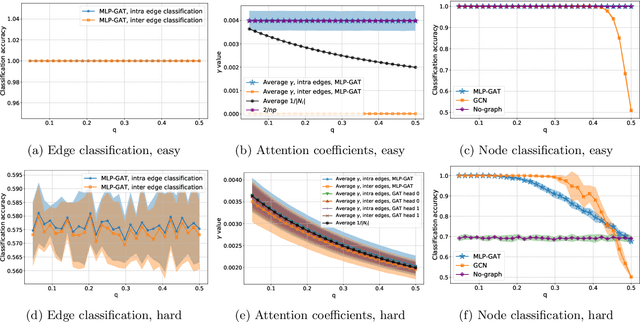
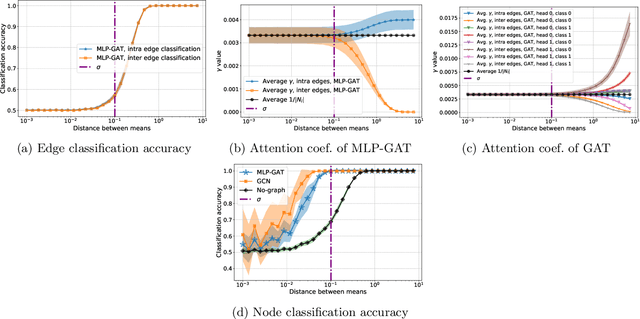
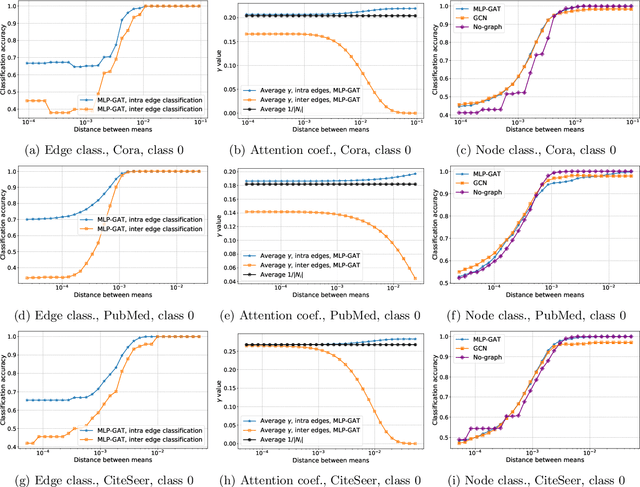
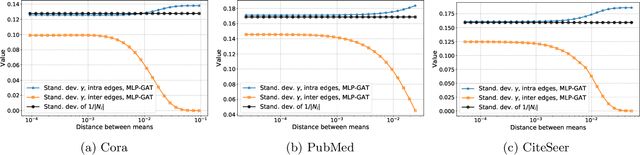
Graph-based learning is a rapidly growing sub-field of machine learning with applications in social networks, citation networks, and bioinformatics. One of the most popular type of models is graph attention networks. These models were introduced to allow a node to aggregate information from the features of neighbor nodes in a non-uniform way in contrast to simple graph convolution which does not distinguish the neighbors of a node. In this paper, we study theoretically this expected behaviour of graph attention networks. We prove multiple results on the performance of the graph attention mechanism for the problem of node classification for a contextual stochastic block model. Here the features of the nodes are obtained from a mixture of Gaussians and the edges from a stochastic block model where the features and the edges are coupled in a natural way. First, we show that in an "easy" regime, where the distance between the means of the Gaussians is large enough, graph attention maintains the weights of intra-class edges and significantly reduces the weights of the inter-class edges. As a corollary, we show that this implies perfect node classification independent of the weights of inter-class edges. However, a classical argument shows that in the "easy" regime, the graph is not needed at all to classify the data with high probability. In the "hard" regime, we show that every attention mechanism fails to distinguish intra-class from inter-class edges. We evaluate our theoretical results on synthetic and real-world data.