Analysis of Corrected Graph Convolutions

Machine learning for node classification on graphs is a prominent area driven by applications such as recommendation systems. State-of-the-art models often use multiple graph convolutions on the data, as empirical evidence suggests they can enhance performance. However, it has been shown empirically and theoretically, that too many graph convolutions can degrade performance significantly, a phenomenon known as oversmoothing. In this paper, we provide a rigorous theoretical analysis, based on the contextual stochastic block model (CSBM), of the performance of vanilla graph convolution from which we remove the principal eigenvector to avoid oversmoothing. We perform a spectral analysis for $k$ rounds of corrected graph convolutions, and we provide results for partial and exact classification. For partial classification, we show that each round of convolution can reduce the misclassification error exponentially up to a saturation level, after which performance does not worsen. For exact classification, we show that the separability threshold can be improved exponentially up to $O({\log{n}}/{\log\log{n}})$ corrected convolutions.

Optimality of Message-Passing Architectures for Sparse Graphs

We study the node classification problem on feature-decorated graphs in the sparse setting, i.e., when the expected degree of a node is $O(1)$ in the number of nodes. Such graphs are typically known to be locally tree-like. We introduce a notion of Bayes optimality for node classification tasks, called asymptotic local Bayes optimality, and compute the optimal classifier according to this criterion for a fairly general statistical data model with arbitrary distributions of the node features and edge connectivity. The optimal classifier is implementable using a message-passing graph neural network architecture. We then compute the generalization error of this classifier and compare its performance against existing learning methods theoretically on a well-studied statistical model with naturally identifiable signal-to-noise ratios (SNRs) in the data. We find that the optimal message-passing architecture interpolates between a standard MLP in the regime of low graph signal and a typical convolution in the regime of high graph signal. Furthermore, we prove a corresponding non-asymptotic result.

Effects of Graph Convolutions in Deep Networks

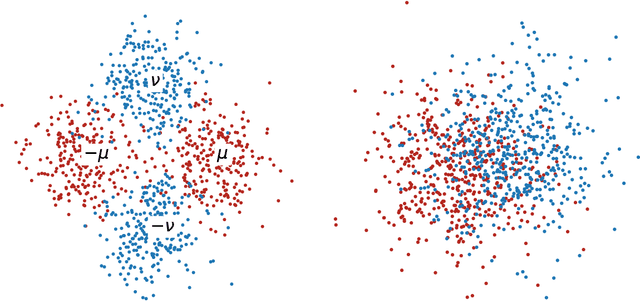
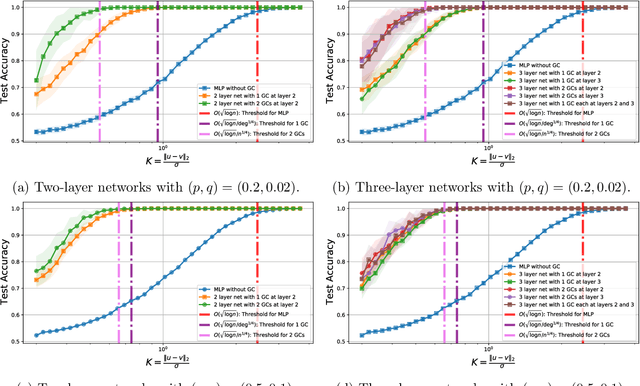
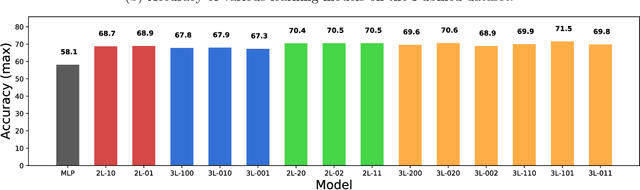
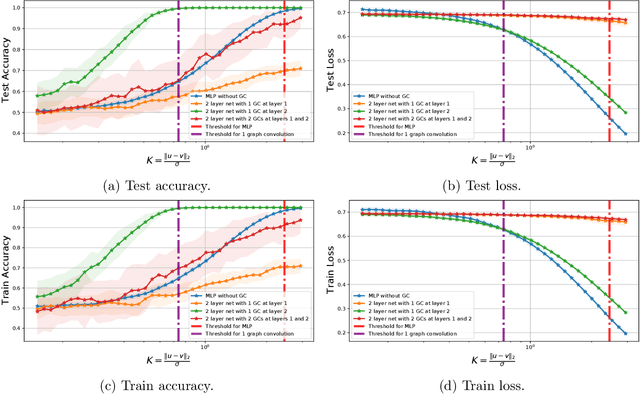
Graph Convolutional Networks (GCNs) are one of the most popular architectures that are used to solve classification problems accompanied by graphical information. We present a rigorous theoretical understanding of the effects of graph convolutions in multi-layer networks. We study these effects through the node classification problem of a non-linearly separable Gaussian mixture model coupled with a stochastic block model. First, we show that a single graph convolution expands the regime of the distance between the means where multi-layer networks can classify the data by a factor of at least $1/\sqrt[4]{\mathbb{E}{\rm deg}}$, where $\mathbb{E}{\rm deg}$ denotes the expected degree of a node. Second, we show that with a slightly stronger graph density, two graph convolutions improve this factor to at least $1/\sqrt[4]{n}$, where $n$ is the number of nodes in the graph. Finally, we provide both theoretical and empirical insights into the performance of graph convolutions placed in different combinations among the layers of a network, concluding that the performance is mutually similar for all combinations of the placement. We present extensive experiments on both synthetic and real-world data that illustrate our results.

Graph Attention Retrospective

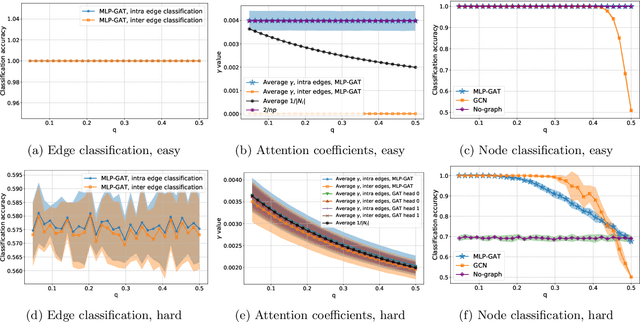
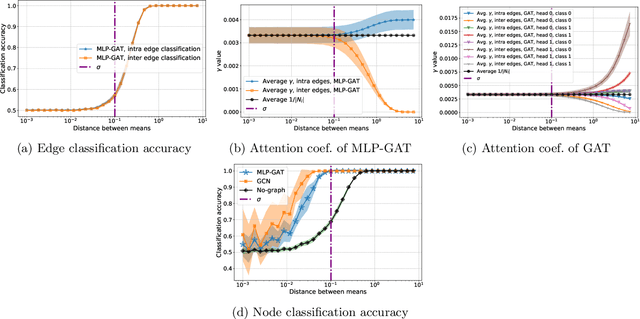
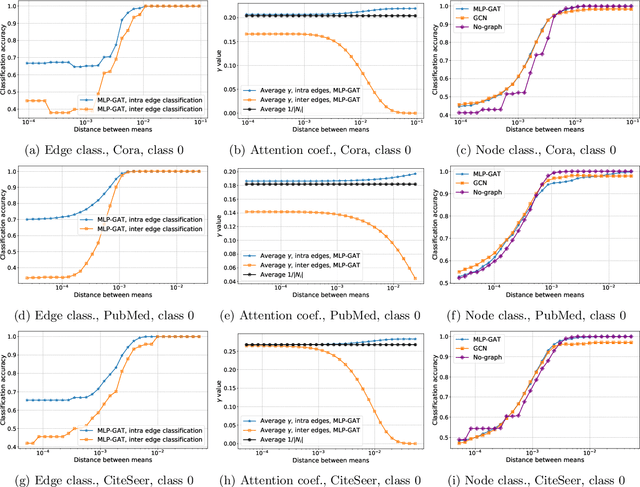
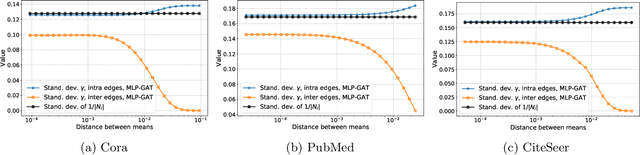
Graph-based learning is a rapidly growing sub-field of machine learning with applications in social networks, citation networks, and bioinformatics. One of the most popular type of models is graph attention networks. These models were introduced to allow a node to aggregate information from the features of neighbor nodes in a non-uniform way in contrast to simple graph convolution which does not distinguish the neighbors of a node. In this paper, we study theoretically this expected behaviour of graph attention networks. We prove multiple results on the performance of the graph attention mechanism for the problem of node classification for a contextual stochastic block model. Here the features of the nodes are obtained from a mixture of Gaussians and the edges from a stochastic block model where the features and the edges are coupled in a natural way. First, we show that in an "easy" regime, where the distance between the means of the Gaussians is large enough, graph attention maintains the weights of intra-class edges and significantly reduces the weights of the inter-class edges. As a corollary, we show that this implies perfect node classification independent of the weights of inter-class edges. However, a classical argument shows that in the "easy" regime, the graph is not needed at all to classify the data with high probability. In the "hard" regime, we show that every attention mechanism fails to distinguish intra-class from inter-class edges. We evaluate our theoretical results on synthetic and real-world data.

Graph Convolution for Semi-Supervised Classification: Improved Linear Separability and Out-of-Distribution Generalization

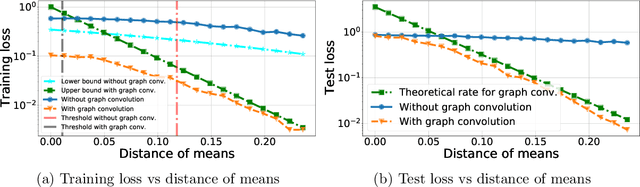
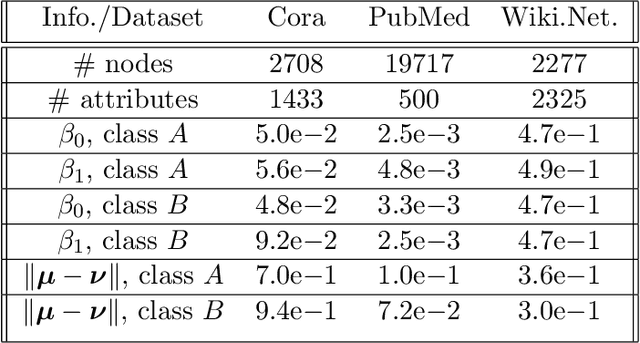
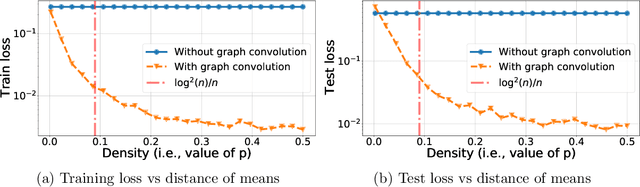
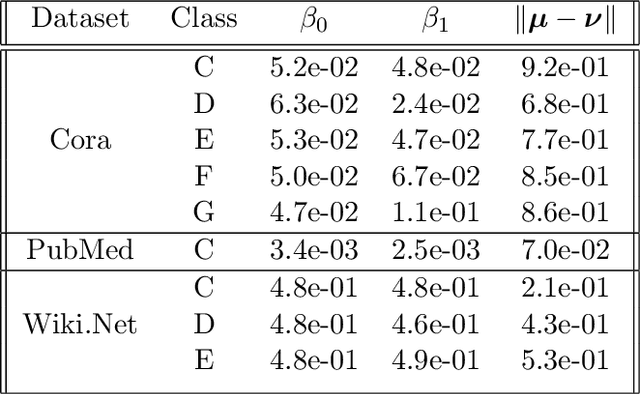
Recently there has been increased interest in semi-supervised classification in the presence of graphical information. A new class of learning models has emerged that relies, at its most basic level, on classifying the data after first applying a graph convolution. To understand the merits of this approach, we study the classification of a mixture of Gaussians, where the data corresponds to the node attributes of a stochastic block model. We show that graph convolution extends the regime in which the data is linearly separable by a factor of roughly $1/\sqrt{D}$, where $D$ is the expected degree of a node, as compared to the mixture model data on its own. Furthermore, we find that the linear classifier obtained by minimizing the cross-entropy loss after the graph convolution generalizes to out-of-distribution data where the unseen data can have different intra- and inter-class edge probabilities from the training data.