Deep Equilibrium Algorithmic Reasoning

Neural Algorithmic Reasoning (NAR) research has demonstrated that graph neural networks (GNNs) could learn to execute classical algorithms. However, most previous approaches have always used a recurrent architecture, where each iteration of the GNN matches an iteration of the algorithm. In this paper we study neurally solving algorithms from a different perspective: since the algorithm's solution is often an equilibrium, it is possible to find the solution directly by solving an equilibrium equation. Our approach requires no information on the ground-truth number of steps of the algorithm, both during train and test time. Furthermore, the proposed method improves the performance of GNNs on executing algorithms and is a step towards speeding up existing NAR models. Our empirical evidence, leveraging algorithms from the CLRS-30 benchmark, validates that one can train a network to solve algorithmic problems by directly finding the equilibrium. We discuss the practical implementation of such models and propose regularisations to improve the performance of these equilibrium reasoners.

Neural Algorithmic Reasoning with Multiple Correct Solutions

Neural Algorithmic Reasoning (NAR) aims to optimize classical algorithms. However, canonical implementations of NAR train neural networks to return only a single solution, even when there are multiple correct solutions to a problem, such as single-source shortest paths. For some applications, it is desirable to recover more than one correct solution. To that end, we give the first method for NAR with multiple solutions. We demonstrate our method on two classical algorithms: Bellman-Ford (BF) and Depth-First Search (DFS), favouring deeper insight into two algorithms over a broader survey of algorithms. This method involves generating appropriate training data as well as sampling and validating solutions from model output. Each step of our method, which can serve as a framework for neural algorithmic reasoning beyond the tasks presented in this paper, might be of independent interest to the field and our results represent the first attempt at this task in the NAR literature.

The Deep Equilibrium Algorithmic Reasoner

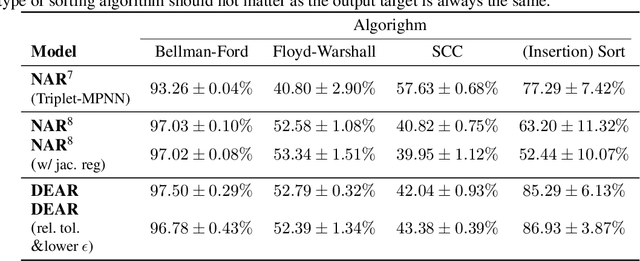
Recent work on neural algorithmic reasoning has demonstrated that graph neural networks (GNNs) could learn to execute classical algorithms. Doing so, however, has always used a recurrent architecture, where each iteration of the GNN aligns with an algorithm's iteration. Since an algorithm's solution is often an equilibrium, we conjecture and empirically validate that one can train a network to solve algorithmic problems by directly finding the equilibrium. Note that this does not require matching each GNN iteration with a step of the algorithm.

Parallel Algorithms Align with Neural Execution

Neural algorithmic reasoners are parallel processors. Teaching them sequential algorithms contradicts this nature, rendering a significant share of their computations redundant. Parallel algorithms however may exploit their full computational power, therefore requiring fewer layers to be executed. This drastically reduces training times, as we observe when comparing parallel implementations of searching, sorting and finding strongly connected components to their sequential counterparts on the CLRS framework. Additionally, parallel versions achieve strongly superior predictive performance in most cases.

Global Concept-Based Interpretability for Graph Neural Networks via Neuron Analysis

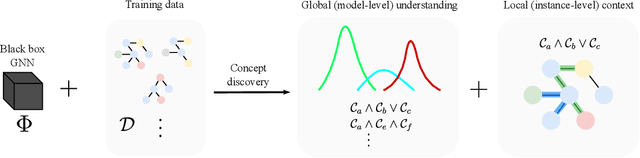
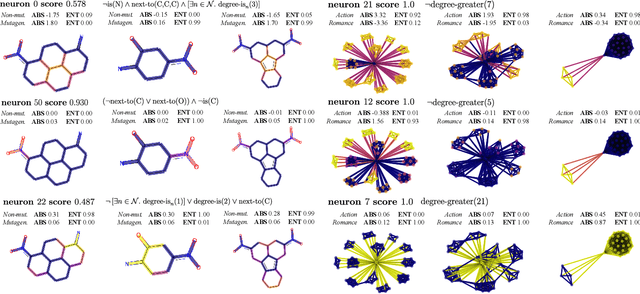
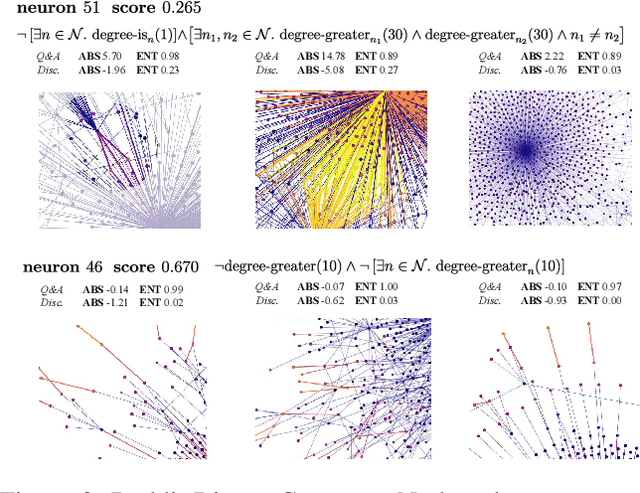
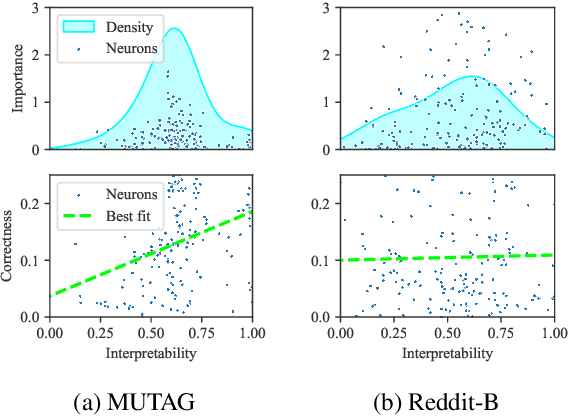
Graph neural networks (GNNs) are highly effective on a variety of graph-related tasks; however, they lack interpretability and transparency. Current explainability approaches are typically local and treat GNNs as black-boxes. They do not look inside the model, inhibiting human trust in the model and explanations. Motivated by the ability of neurons to detect high-level semantic concepts in vision models, we perform a novel analysis on the behaviour of individual GNN neurons to answer questions about GNN interpretability, and propose new metrics for evaluating the interpretability of GNN neurons. We propose a novel approach for producing global explanations for GNNs using neuron-level concepts to enable practitioners to have a high-level view of the model. Specifically, (i) to the best of our knowledge, this is the first work which shows that GNN neurons act as concept detectors and have strong alignment with concepts formulated as logical compositions of node degree and neighbourhood properties; (ii) we quantitatively assess the importance of detected concepts, and identify a trade-off between training duration and neuron-level interpretability; (iii) we demonstrate that our global explainability approach has advantages over the current state-of-the-art -- we can disentangle the explanation into individual interpretable concepts backed by logical descriptions, which reduces potential for bias and improves user-friendliness.

HEAT: Hyperedge Attention Networks

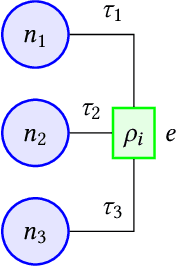
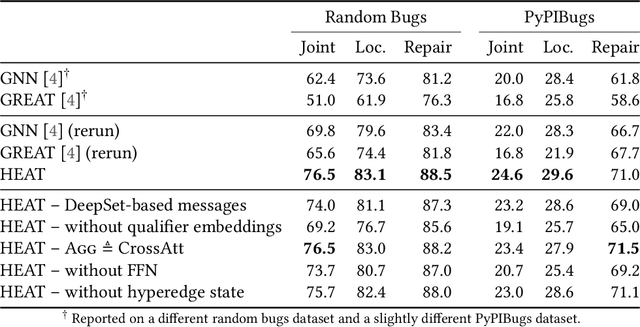
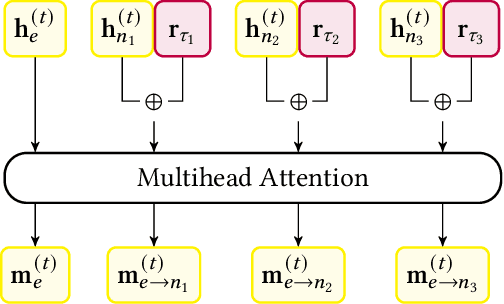
Learning from structured data is a core machine learning task. Commonly, such data is represented as graphs, which normally only consider (typed) binary relationships between pairs of nodes. This is a substantial limitation for many domains with highly-structured data. One important such domain is source code, where hypergraph-based representations can better capture the semantically rich and structured nature of code. In this work, we present HEAT, a neural model capable of representing typed and qualified hypergraphs, where each hyperedge explicitly qualifies how participating nodes contribute. It can be viewed as a generalization of both message passing neural networks and Transformers. We evaluate HEAT on knowledge base completion and on bug detection and repair using a novel hypergraph representation of programs. In both settings, it outperforms strong baselines, indicating its power and generality.

Algorithmic Concept-based Explainable Reasoning

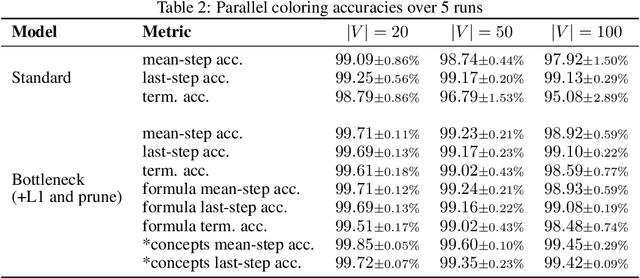
Recent research on graph neural network (GNN) models successfully applied GNNs to classical graph algorithms and combinatorial optimisation problems. This has numerous benefits, such as allowing applications of algorithms when preconditions are not satisfied, or reusing learned models when sufficient training data is not available or can't be generated. Unfortunately, a key hindrance of these approaches is their lack of explainability, since GNNs are black-box models that cannot be interpreted directly. In this work, we address this limitation by applying existing work on concept-based explanations to GNN models. We introduce concept-bottleneck GNNs, which rely on a modification to the GNN readout mechanism. Using three case studies we demonstrate that: (i) our proposed model is capable of accurately learning concepts and extracting propositional formulas based on the learned concepts for each target class; (ii) our concept-based GNN models achieve comparative performance with state-of-the-art models; (iii) we can derive global graph concepts, without explicitly providing any supervision on graph-level concepts.

LENs: a Python library for Logic Explained Networks

LENs is a Python module integrating a variety of state-of-the-art approaches to provide logic explanations from neural networks. This package focuses on bringing these methods to non-specialists. It has minimal dependencies and it is distributed under the Apache 2.0 licence allowing both academic and commercial use. Source code and documentation can be downloaded from the github repository: https://github.com/pietrobarbiero/logic_explainer_networks.

Neural Bipartite Matching

Graph neural networks (GNNs) have found application for learning in the space of algorithms. However, the algorithms chosen by existing research (sorting, Breadth-First search, shortest path finding, etc.) usually align perfectly with a standard GNN architecture. This report describes how neural execution is applied to a complex algorithm, such as finding maximum bipartite matching by reducing it to a flow problem and using Ford-Fulkerson to find the maximum flow. This is achieved via neural execution based only on features generated from a single GNN. The evaluation shows strongly generalising results with the network achieving optimal matching almost 100% of the time.