CliquePH: Higher-Order Information for Graph Neural Networks through Persistent Homology on Clique Graphs
Paper and Code
Sep 12, 2024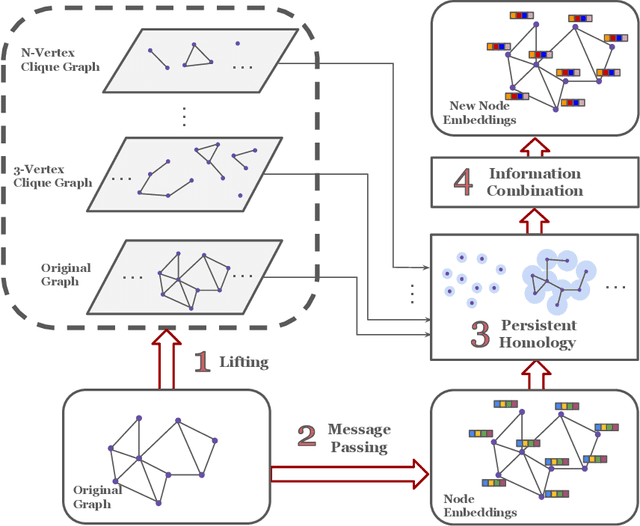
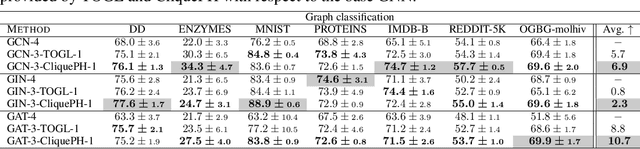
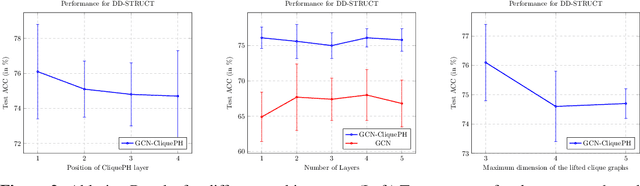

Graph neural networks have become the default choice by practitioners for graph learning tasks such as graph classification and node classification. Nevertheless, popular graph neural network models still struggle to capture higher-order information, i.e., information that goes \emph{beyond} pairwise interactions. Recent work has shown that persistent homology, a tool from topological data analysis, can enrich graph neural networks with topological information that they otherwise could not capture. Calculating such features is efficient for dimension 0 (connected components) and dimension 1 (cycles). However, when it comes to higher-order structures, it does not scale well, with a complexity of $O(n^d)$, where $n$ is the number of nodes and $d$ is the order of the structures. In this work, we introduce a novel method that extracts information about higher-order structures in the graph while still using the efficient low-dimensional persistent homology algorithm. On standard benchmark datasets, we show that our method can lead to up to $31\%$ improvements in test accuracy.
 Add to Chrome
Add to Chrome Add to Firefox
Add to Firefox Add to Edge
Add to Edge