MANTRA: The Manifold Triangulations Assemblage

The rising interest in leveraging higher-order interactions present in complex systems has led to a surge in more expressive models exploiting high-order structures in the data, especially in topological deep learning (TDL), which designs neural networks on high-order domains such as simplicial complexes. However, progress in this field is hindered by the scarcity of datasets for benchmarking these architectures. To address this gap, we introduce MANTRA, the first large-scale, diverse, and intrinsically high order dataset for benchmarking high-order models, comprising over 43,000 and 249,000 triangulations of surfaces and three-dimensional manifolds, respectively. With MANTRA, we assess several graph- and simplicial complex-based models on three topological classification tasks. We demonstrate that while simplicial complex-based neural networks generally outperform their graph-based counterparts in capturing simple topological invariants, they also struggle, suggesting a rethink of TDL. Thus, MANTRA serves as a benchmark for assessing and advancing topological methods, leading the way for more effective high-order models.

Attending to Topological Spaces: The Cellular Transformer

Topological Deep Learning seeks to enhance the predictive performance of neural network models by harnessing topological structures in input data. Topological neural networks operate on spaces such as cell complexes and hypergraphs, that can be seen as generalizations of graphs. In this work, we introduce the Cellular Transformer (CT), a novel architecture that generalizes graph-based transformers to cell complexes. First, we propose a new formulation of the usual self- and cross-attention mechanisms, tailored to leverage incidence relations in cell complexes, e.g., edge-face and node-edge relations. Additionally, we propose a set of topological positional encodings specifically designed for cell complexes. By transforming three graph datasets into cell complex datasets, our experiments reveal that CT not only achieves state-of-the-art performance, but it does so without the need for more complex enhancements such as virtual nodes, in-domain structural encodings, or graph rewiring.

Topological Data Analysis for Neural Network Analysis: A Comprehensive Survey

This survey provides a comprehensive exploration of applications of Topological Data Analysis (TDA) within neural network analysis. Using TDA tools such as persistent homology and Mapper, we delve into the intricate structures and behaviors of neural networks and their datasets. We discuss different strategies to obtain topological information from data and neural networks by means of TDA. Additionally, we review how topological information can be leveraged to analyze properties of neural networks, such as their generalization capacity or expressivity. We explore practical implications of deep learning, specifically focusing on areas like adversarial detection and model selection. Our survey organizes the examined works into four broad domains: 1. Characterization of neural network architectures; 2. Analysis of decision regions and boundaries; 3. Study of internal representations, activations, and parameters; 4. Exploration of training dynamics and loss functions. Within each category, we discuss several articles, offering background information to aid in understanding the various methodologies. We conclude with a synthesis of key insights gained from our study, accompanied by a discussion of challenges and potential advancements in the field.

Decorrelating neurons using persistence

We propose a novel way to improve the generalisation capacity of deep learning models by reducing high correlations between neurons. For this, we present two regularisation terms computed from the weights of a minimum spanning tree of the clique whose vertices are the neurons of a given network (or a sample of those), where weights on edges are correlation dissimilarities. We provide an extensive set of experiments to validate the effectiveness of our terms, showing that they outperform popular ones. Also, we demonstrate that naive minimisation of all correlations between neurons obtains lower accuracies than our regularisation terms, suggesting that redundancies play a significant role in artificial neural networks, as evidenced by some studies in neuroscience for real networks. We include a proof of differentiability of our regularisers, thus developing the first effective topological persistence-based regularisation terms that consider the whole set of neurons and that can be applied to a feedforward architecture in any deep learning task such as classification, data generation, or regression.

A topological classifier to characterize brain states: When shape matters more than variance

Despite the remarkable accuracies attained by machine learning classifiers to separate complex datasets in a supervised fashion, most of their operation falls short to provide an informed intuition about the structure of data, and, what is more important, about the phenomena being characterized by the given datasets. By contrast, topological data analysis (TDA) is devoted to study the shape of data clouds by means of persistence descriptors and provides a quantitative characterization of specific topological features of the dataset under scrutiny. In this article we introduce a novel TDA-based classifier that works on the principle of assessing quantifiable changes on topological metrics caused by the addition of new input to a subset of data. We used this classifier with a high-dimensional electro-encephalographic (EEG) dataset recorded from eleven participants during a decision-making experiment in which three motivational states were induced through a manipulation of social pressure. After processing a band-pass filtered version of EEG signals, we calculated silhouettes from persistence diagrams associated with each motivated state, and classified unlabeled signals according to their impact on each reference silhouette. Our results show that in addition to providing accuracies within the range of those of a nearest neighbour classifier, the TDA classifier provides formal intuition of the structure of the dataset as well as an estimate of its intrinsic dimension. Towards this end, we incorporated dimensionality reduction methods to our procedure and found that the accuracy of our TDA classifier is generally not sensitive to explained variance but rather to shape, contrary to what happens with most machine learning classifiers.

Importance attribution in neural networks by means of persistence landscapes of time series

We propose and implement a method to analyze time series with a neural network using a matrix of area-normalized persistence landscapes obtained through topological data analysis. We include a gating layer in the network's architecture that is able to identify the most relevant landscape levels for the classification task, thus working as an importance attribution system. Next, we perform a matching between the selected landscape functions and the corresponding critical points of the original time series. From this matching we are able to reconstruct an approximate shape of the time series that gives insight into the classification decision. We test this technique with input data from a dataset of electrocardiographic signals.

Towards explaining the generalization gap in neural networks using topological data analysis

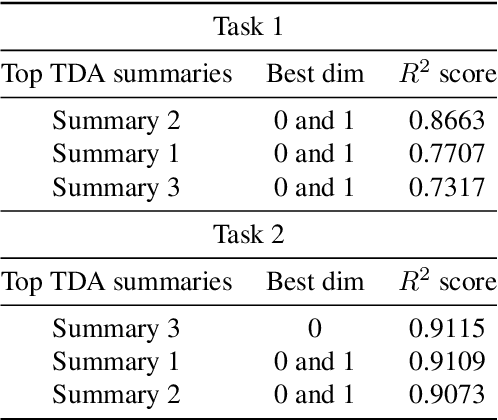
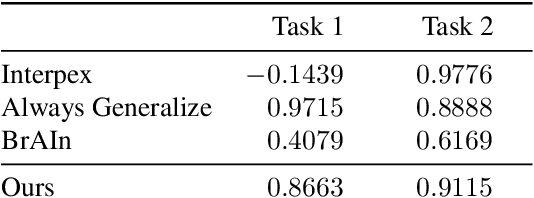
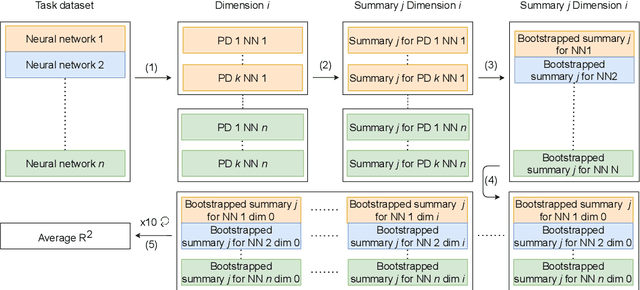
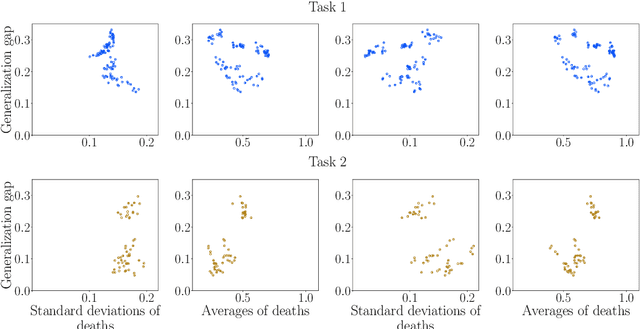
Understanding how neural networks generalize on unseen data is crucial for designing more robust and reliable models. In this paper, we study the generalization gap of neural networks using methods from topological data analysis. For this purpose, we compute homological persistence diagrams of weighted graphs constructed from neuron activation correlations after a training phase, aiming to capture patterns that are linked to the generalization capacity of the network. We compare the usefulness of different numerical summaries from persistence diagrams and show that a combination of some of them can accurately predict and partially explain the generalization gap without the need of a test set. Evaluation on two computer vision recognition tasks (CIFAR10 and SVHN) shows competitive generalization gap prediction when compared against state-of-the-art methods.

Reconstruction of univariate functions from directional persistence diagrams

We describe a method for approximating a single-variable function $f$ using persistence diagrams of sublevel sets of $f$ from height functions in different directions. We provide algorithms for the piecewise linear case and for the smooth case. Three directions suffice to locate all local maxima and minima of a piecewise linear continuous function from its collection of directional persistence diagrams, while five directions are needed in the case of smooth functions with non-degenerate critical points. Our approximation of functions by means of persistence diagrams is motivated by a study of importance attribution in machine learning, where one seeks to reduce the number of critical points of signal functions without a significant loss of information for a neural network classifier.