MANTRA: The Manifold Triangulations Assemblage

The rising interest in leveraging higher-order interactions present in complex systems has led to a surge in more expressive models exploiting high-order structures in the data, especially in topological deep learning (TDL), which designs neural networks on high-order domains such as simplicial complexes. However, progress in this field is hindered by the scarcity of datasets for benchmarking these architectures. To address this gap, we introduce MANTRA, the first large-scale, diverse, and intrinsically high order dataset for benchmarking high-order models, comprising over 43,000 and 249,000 triangulations of surfaces and three-dimensional manifolds, respectively. With MANTRA, we assess several graph- and simplicial complex-based models on three topological classification tasks. We demonstrate that while simplicial complex-based neural networks generally outperform their graph-based counterparts in capturing simple topological invariants, they also struggle, suggesting a rethink of TDL. Thus, MANTRA serves as a benchmark for assessing and advancing topological methods, leading the way for more effective high-order models.

Attending to Topological Spaces: The Cellular Transformer

Topological Deep Learning seeks to enhance the predictive performance of neural network models by harnessing topological structures in input data. Topological neural networks operate on spaces such as cell complexes and hypergraphs, that can be seen as generalizations of graphs. In this work, we introduce the Cellular Transformer (CT), a novel architecture that generalizes graph-based transformers to cell complexes. First, we propose a new formulation of the usual self- and cross-attention mechanisms, tailored to leverage incidence relations in cell complexes, e.g., edge-face and node-edge relations. Additionally, we propose a set of topological positional encodings specifically designed for cell complexes. By transforming three graph datasets into cell complex datasets, our experiments reveal that CT not only achieves state-of-the-art performance, but it does so without the need for more complex enhancements such as virtual nodes, in-domain structural encodings, or graph rewiring.

Topological Data Analysis for Neural Network Analysis: A Comprehensive Survey

This survey provides a comprehensive exploration of applications of Topological Data Analysis (TDA) within neural network analysis. Using TDA tools such as persistent homology and Mapper, we delve into the intricate structures and behaviors of neural networks and their datasets. We discuss different strategies to obtain topological information from data and neural networks by means of TDA. Additionally, we review how topological information can be leveraged to analyze properties of neural networks, such as their generalization capacity or expressivity. We explore practical implications of deep learning, specifically focusing on areas like adversarial detection and model selection. Our survey organizes the examined works into four broad domains: 1. Characterization of neural network architectures; 2. Analysis of decision regions and boundaries; 3. Study of internal representations, activations, and parameters; 4. Exploration of training dynamics and loss functions. Within each category, we discuss several articles, offering background information to aid in understanding the various methodologies. We conclude with a synthesis of key insights gained from our study, accompanied by a discussion of challenges and potential advancements in the field.

ICML 2023 Topological Deep Learning Challenge : Design and Results

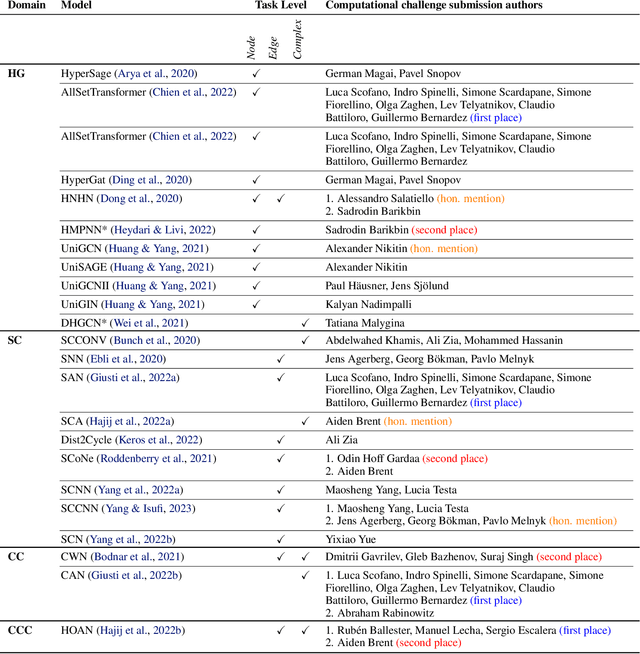
This paper presents the computational challenge on topological deep learning that was hosted within the ICML 2023 Workshop on Topology and Geometry in Machine Learning. The competition asked participants to provide open-source implementations of topological neural networks from the literature by contributing to the python packages TopoNetX (data processing) and TopoModelX (deep learning). The challenge attracted twenty-eight qualifying submissions in its two-month duration. This paper describes the design of the challenge and summarizes its main findings.

Decorrelating neurons using persistence

We propose a novel way to improve the generalisation capacity of deep learning models by reducing high correlations between neurons. For this, we present two regularisation terms computed from the weights of a minimum spanning tree of the clique whose vertices are the neurons of a given network (or a sample of those), where weights on edges are correlation dissimilarities. We provide an extensive set of experiments to validate the effectiveness of our terms, showing that they outperform popular ones. Also, we demonstrate that naive minimisation of all correlations between neurons obtains lower accuracies than our regularisation terms, suggesting that redundancies play a significant role in artificial neural networks, as evidenced by some studies in neuroscience for real networks. We include a proof of differentiability of our regularisers, thus developing the first effective topological persistence-based regularisation terms that consider the whole set of neurons and that can be applied to a feedforward architecture in any deep learning task such as classification, data generation, or regression.

Towards explaining the generalization gap in neural networks using topological data analysis

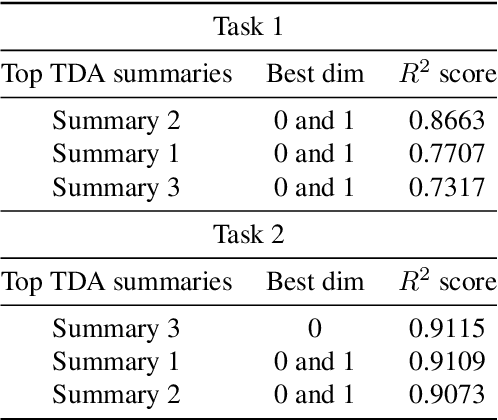
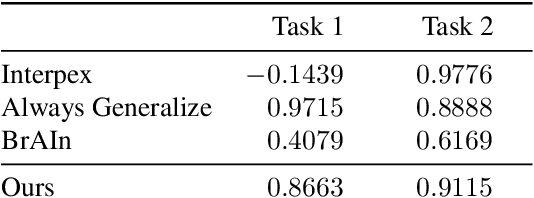
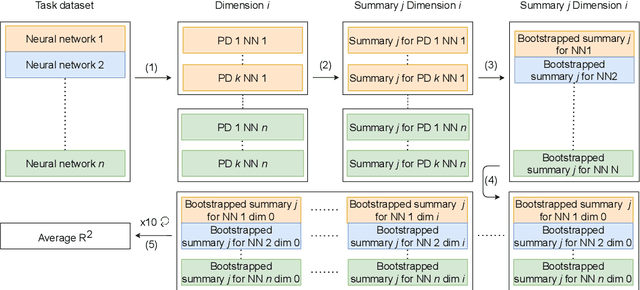
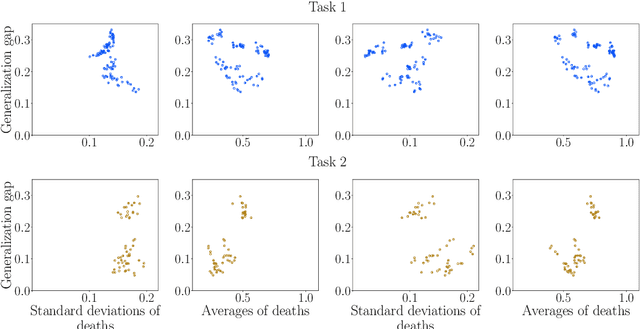
Understanding how neural networks generalize on unseen data is crucial for designing more robust and reliable models. In this paper, we study the generalization gap of neural networks using methods from topological data analysis. For this purpose, we compute homological persistence diagrams of weighted graphs constructed from neuron activation correlations after a training phase, aiming to capture patterns that are linked to the generalization capacity of the network. We compare the usefulness of different numerical summaries from persistence diagrams and show that a combination of some of them can accurately predict and partially explain the generalization gap without the need of a test set. Evaluation on two computer vision recognition tasks (CIFAR10 and SVHN) shows competitive generalization gap prediction when compared against state-of-the-art methods.