MANTRA: The Manifold Triangulations Assemblage

The rising interest in leveraging higher-order interactions present in complex systems has led to a surge in more expressive models exploiting high-order structures in the data, especially in topological deep learning (TDL), which designs neural networks on high-order domains such as simplicial complexes. However, progress in this field is hindered by the scarcity of datasets for benchmarking these architectures. To address this gap, we introduce MANTRA, the first large-scale, diverse, and intrinsically high order dataset for benchmarking high-order models, comprising over 43,000 and 249,000 triangulations of surfaces and three-dimensional manifolds, respectively. With MANTRA, we assess several graph- and simplicial complex-based models on three topological classification tasks. We demonstrate that while simplicial complex-based neural networks generally outperform their graph-based counterparts in capturing simple topological invariants, they also struggle, suggesting a rethink of TDL. Thus, MANTRA serves as a benchmark for assessing and advancing topological methods, leading the way for more effective high-order models.

A Diffusion Model Predicts 3D Shapes from 2D Microscopy Images

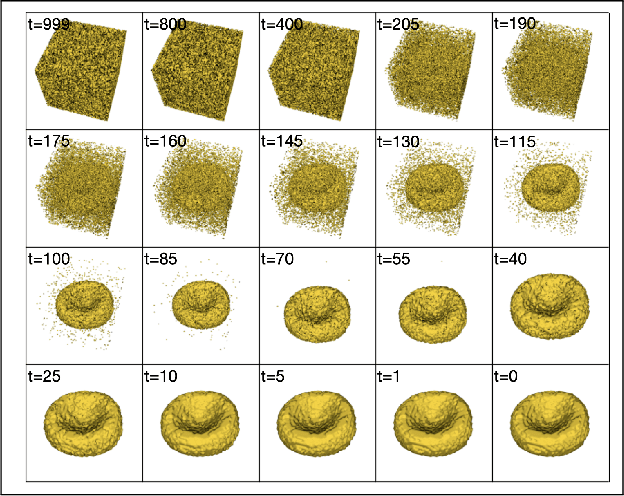
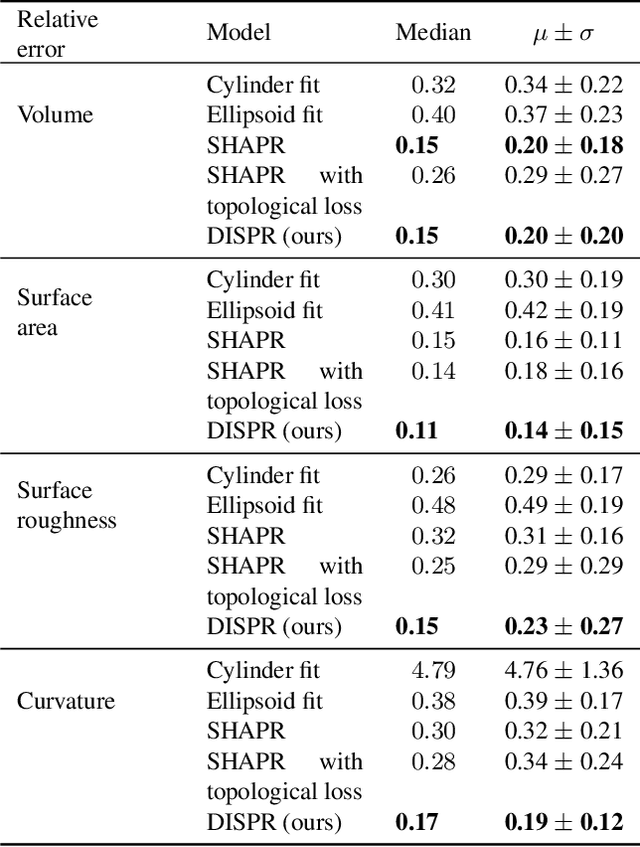
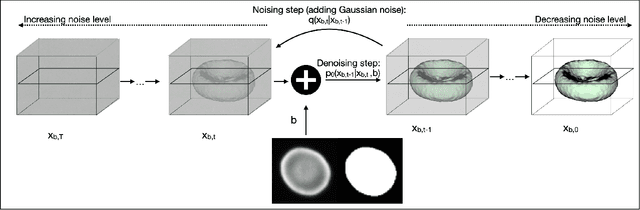
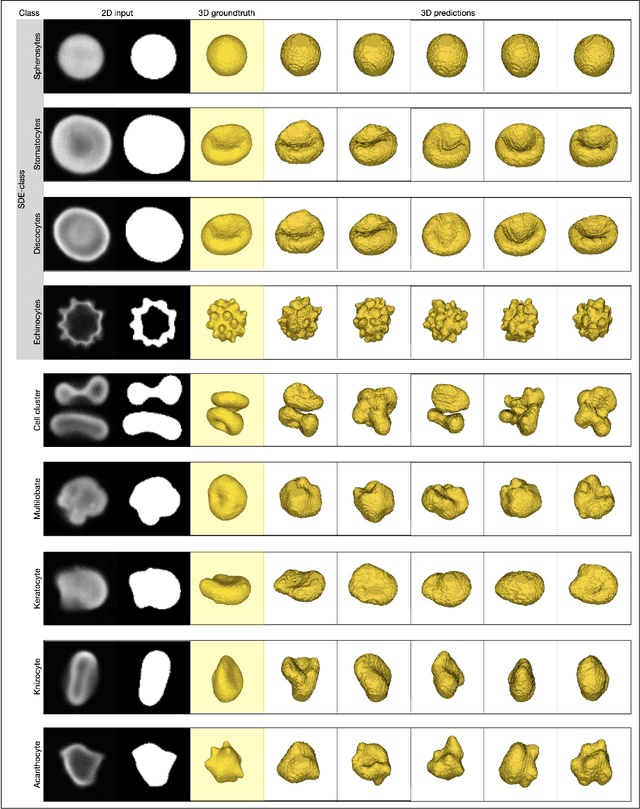
Diffusion models are a class of generative models, showing superior performance as compared to other generative models in creating realistic images when trained on natural image datasets. We introduce DISPR, a diffusion-based model for solving the inverse problem of three-dimensional (3D) cell shape prediction from two-dimensional (2D) single cell microscopy images. Using the 2D microscopy image as a prior, DISPR is conditioned to predict realistic 3D shape reconstructions. To showcase the applicability of DISPR as a data augmentation tool in a feature-based single cell classification task, we extract morphological features from the cells grouped into six highly imbalanced classes. Adding features from predictions of DISPR to the three minority classes improved the macro F1 score from $F1_\text{macro} = 55.2 \pm 4.6\%$ to $F1_\text{macro} = 72.2 \pm 4.9\%$. With our method being the first to employ a diffusion-based model in this context, we demonstrate that diffusion models can be applied to inverse problems in 3D, and that they learn to reconstruct 3D shapes with realistic morphological features from 2D microscopy images.