Prediction-powered Generalization of Causal Inferences

Causal inferences from a randomized controlled trial (RCT) may not pertain to a target population where some effect modifiers have a different distribution. Prior work studies generalizing the results of a trial to a target population with no outcome but covariate data available. We show how the limited size of trials makes generalization a statistically infeasible task, as it requires estimating complex nuisance functions. We develop generalization algorithms that supplement the trial data with a prediction model learned from an additional observational study (OS), without making any assumptions on the OS. We theoretically and empirically show that our methods facilitate better generalization when the OS is high-quality, and remain robust when it is not, and e.g., have unmeasured confounding.

Recent Advances, Applications, and Open Challenges in Machine Learning for Health: Reflections from Research Roundtables at ML4H 2023 Symposium

The third ML4H symposium was held in person on December 10, 2023, in New Orleans, Louisiana, USA. The symposium included research roundtable sessions to foster discussions between participants and senior researchers on timely and relevant topics for the \ac{ML4H} community. Encouraged by the successful virtual roundtables in the previous year, we organized eleven in-person roundtables and four virtual roundtables at ML4H 2022. The organization of the research roundtables at the conference involved 17 Senior Chairs and 19 Junior Chairs across 11 tables. Each roundtable session included invited senior chairs (with substantial experience in the field), junior chairs (responsible for facilitating the discussion), and attendees from diverse backgrounds with interest in the session's topic. Herein we detail the organization process and compile takeaways from these roundtable discussions, including recent advances, applications, and open challenges for each topic. We conclude with a summary and lessons learned across all roundtables. This document serves as a comprehensive review paper, summarizing the recent advancements in machine learning for healthcare as contributed by foremost researchers in the field.

Benchmarking Observational Studies with Experimental Data under Right-Censoring

Drawing causal inferences from observational studies (OS) requires unverifiable validity assumptions; however, one can falsify those assumptions by benchmarking the OS with experimental data from a randomized controlled trial (RCT). A major limitation of existing procedures is not accounting for censoring, despite the abundance of RCTs and OSes that report right-censored time-to-event outcomes. We consider two cases where censoring time (1) is independent of time-to-event and (2) depends on time-to-event the same way in OS and RCT. For the former, we adopt a censoring-doubly-robust signal for the conditional average treatment effect (CATE) to facilitate an equivalence test of CATEs in OS and RCT, which serves as a proxy for testing if the validity assumptions hold. For the latter, we show that the same test can still be used even though unbiased CATE estimation may not be possible. We verify the effectiveness of our censoring-aware tests via semi-synthetic experiments and analyze RCT and OS data from the Women's Health Initiative study.

Falsification of Internal and External Validity in Observational Studies via Conditional Moment Restrictions

Randomized Controlled Trials (RCT)s are relied upon to assess new treatments, but suffer from limited power to guide personalized treatment decisions. On the other hand, observational (i.e., non-experimental) studies have large and diverse populations, but are prone to various biases (e.g. residual confounding). To safely leverage the strengths of observational studies, we focus on the problem of falsification, whereby RCTs are used to validate causal effect estimates learned from observational data. In particular, we show that, given data from both an RCT and an observational study, assumptions on internal and external validity have an observable, testable implication in the form of a set of Conditional Moment Restrictions (CMRs). Further, we show that expressing these CMRs with respect to the causal effect, or "causal contrast", as opposed to individual counterfactual means, provides a more reliable falsification test. In addition to giving guarantees on the asymptotic properties of our test, we demonstrate superior power and type I error of our approach on semi-synthetic and real world datasets. Our approach is interpretable, allowing a practitioner to visualize which subgroups in the population lead to falsification of an observational study.

Federated Multi-Armed Bandits Under Byzantine Attacks

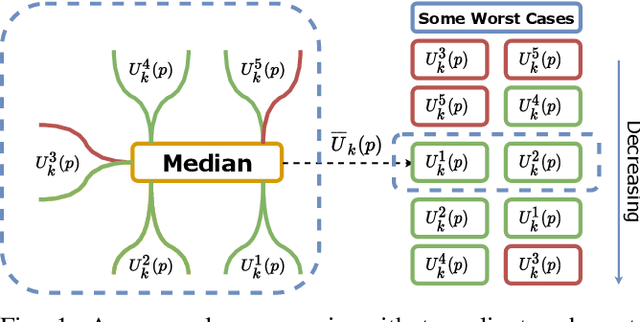
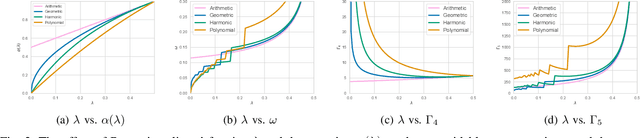
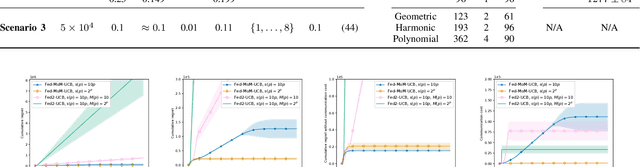
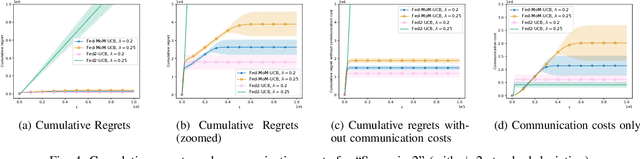
Multi-armed bandits (MAB) is a simple reinforcement learning model where the learner controls the trade-off between exploration versus exploitation to maximize its cumulative reward. Federated multi-armed bandits (FMAB) is a recently emerging framework where a cohort of learners with heterogeneous local models play a MAB game and communicate their aggregated feedback to a parameter server to learn the global feedback model. Federated learning models are vulnerable to adversarial attacks such as model-update attacks or data poisoning. In this work, we study an FMAB problem in the presence of Byzantine clients who can send false model updates that pose a threat to the learning process. We borrow tools from robust statistics and propose a median-of-means-based estimator: Fed-MoM-UCB, to cope with the Byzantine clients. We show that if the Byzantine clients constitute at most half the cohort, it is possible to incur a cumulative regret on the order of ${\cal O} (\log T)$ with respect to an unavoidable error margin, including the communication cost between the clients and the parameter server. We analyze the interplay between the algorithm parameters, unavoidable error margin, regret, communication cost, and the arms' suboptimality gaps. We demonstrate Fed-MoM-UCB's effectiveness against the baselines in the presence of Byzantine attacks via experiments.

Safe Linear Leveling Bandits

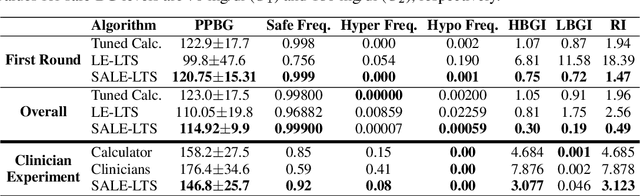
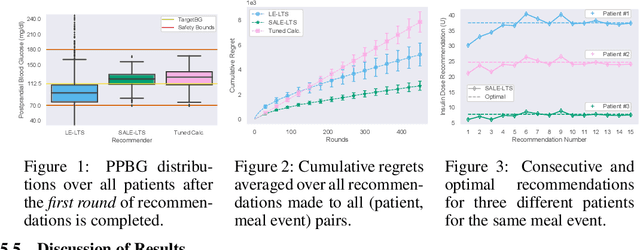
Multi-armed bandits (MAB) are extensively studied in various settings where the objective is to \textit{maximize} the actions' outcomes (i.e., rewards) over time. Since safety is crucial in many real-world problems, safe versions of MAB algorithms have also garnered considerable interest. In this work, we tackle a different critical task through the lens of \textit{linear stochastic bandits}, where the aim is to keep the actions' outcomes close to a target level while respecting a \textit{two-sided} safety constraint, which we call \textit{leveling}. Such a task is prevalent in numerous domains. Many healthcare problems, for instance, require keeping a physiological variable in a range and preferably close to a target level. The radical change in our objective necessitates a new acquisition strategy, which is at the heart of a MAB algorithm. We propose SALE-LTS: Safe Leveling via Linear Thompson Sampling algorithm, with a novel acquisition strategy to accommodate our task and show that it achieves sublinear regret with the same time and dimension dependence as previous works on the classical reward maximization problem absent any safety constraint. We demonstrate and discuss our algorithm's empirical performance in detail via thorough experiments.

ESCADA: Efficient Safety and Context Aware Dose Allocation for Precision Medicine

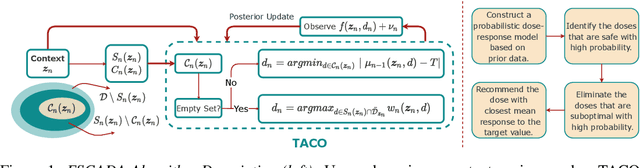
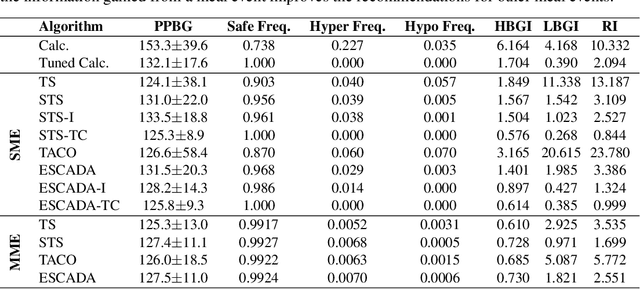
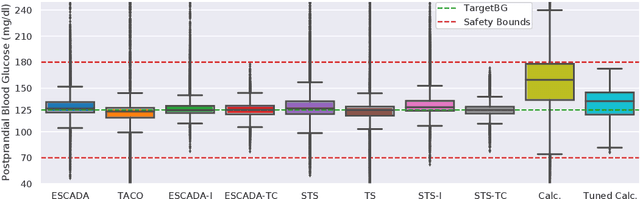
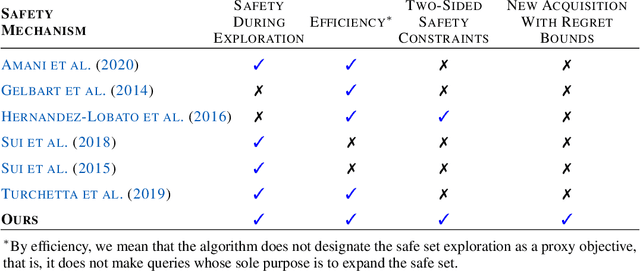
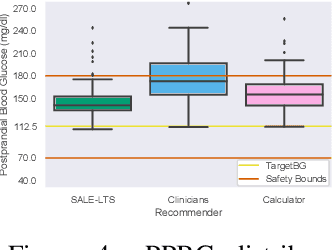
Finding an optimal individualized treatment regimen is considered one of the most challenging precision medicine problems. Various patient characteristics influence the response to the treatment, and hence, there is no one-size-fits-all regimen. Moreover, the administration of even a single unsafe dose during the treatment can have catastrophic consequences on patients' health. Therefore, an individualized treatment model must ensure patient {\em safety} while {\em efficiently} optimizing the course of therapy. In this work, we study a prevalent and essential medical problem setting where the treatment aims to keep a physiological variable in a range, preferably close to a target level. Such a task is relevant in numerous other domains as well. We propose ESCADA, a generic algorithm for this problem structure, to make individualized and context-aware optimal dose recommendations while assuring patient safety. We derive high probability upper bounds on the regret of ESCADA along with safety guarantees. Finally, we make extensive simulations on the {\em bolus insulin dose} allocation problem in type 1 diabetes mellitus disease and compare ESCADA's performance against Thompson sampling's, rule-based dose allocators', and clinicians'.

Distance and Position Estimation in Visible Light Systems with RGB LEDs

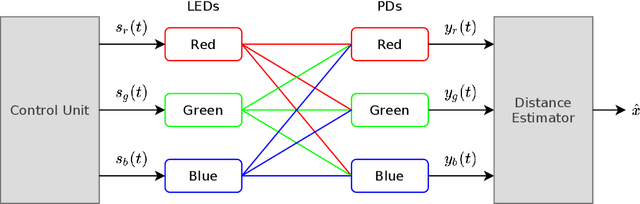
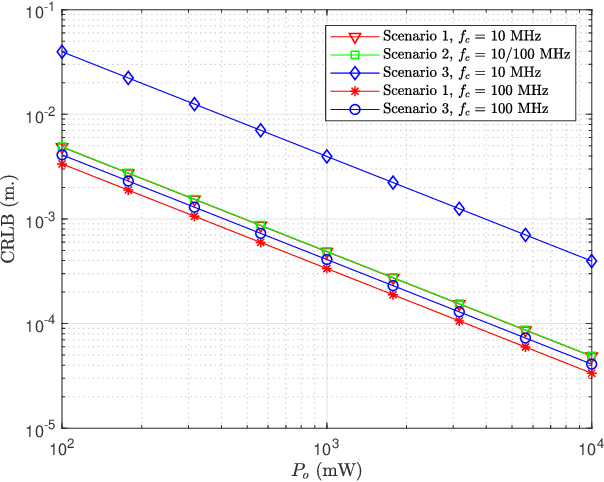
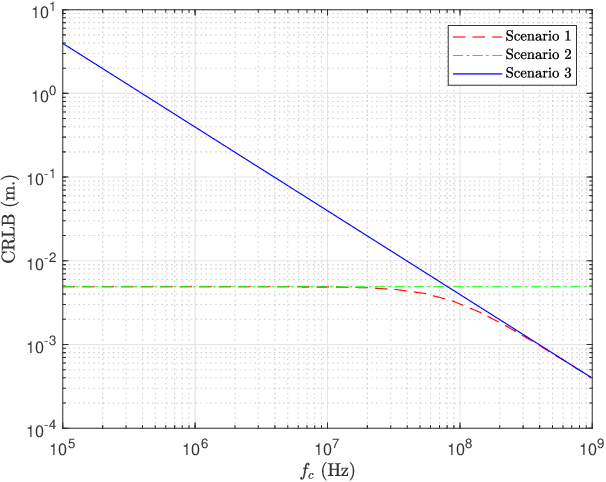
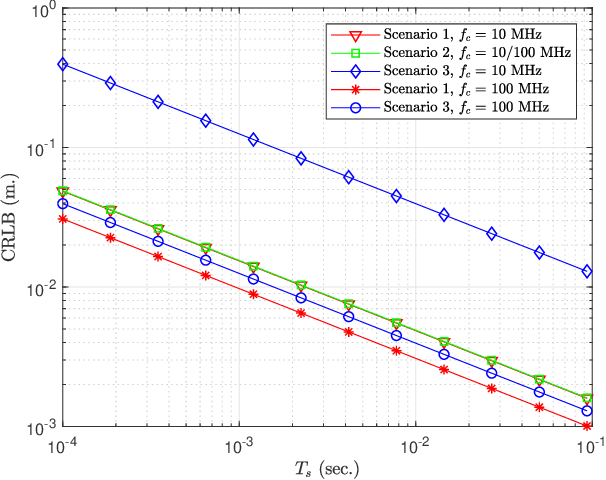
In this manuscript, distance and position estimation problems are investigated for visible light positioning (VLP) systems with red-green-blue (RGB) light emitting diodes (LEDs). The accuracy limits on distance and position estimation are calculated in terms of the Cramer-Rao lower bound (CRLB) for three different scenarios. Scenario~1 and Scenario~2 correspond to synchronous and asynchronous systems, respectively, with known channel attenuation formulas at the receiver. In Scenario~3, a synchronous system is considered but channel attenuation formulas are not known at the receiver. The derived CRLB expressions reveal the relations among distance/position estimation accuracies in the considered scenarios and lead to intuitive explanations for the benefits of using RGB LEDs. In addition, maximum likelihood (ML) estimators are derived in all scenarios, and it is shown that they can achieve close performance to the CRLBs in some cases for sufficiently high source optical powers.