VOPy: A Framework for Black-box Vector Optimization

We introduce VOPy, an open-source Python library designed to address black-box vector optimization, where multiple objectives must be optimized simultaneously with respect to a partial order induced by a convex cone. VOPy extends beyond traditional multi-objective optimization (MOO) tools by enabling flexible, cone-based ordering of solutions; with an application scope that includes environments with observation noise, discrete or continuous design spaces, limited budgets, and batch observations. VOPy provides a modular architecture, facilitating the integration of existing methods and the development of novel algorithms. We detail VOPy's architecture, usage, and potential to advance research and application in the field of vector optimization. The source code for VOPy is available at https://github.com/Bilkent-CYBORG/VOPy.

Vector Optimization with Gaussian Process Bandits

Learning problems in which multiple conflicting objectives must be considered simultaneously often arise in various fields, including engineering, drug design, and environmental management. Traditional methods for dealing with multiple black-box objective functions, such as scalarization and identification of the Pareto set under the componentwise order, have limitations in incorporating objective preferences and exploring the solution space accordingly. While vector optimization offers improved flexibility and adaptability via specifying partial orders based on ordering cones, current techniques designed for sequential experiments either suffer from high sample complexity or lack theoretical guarantees. To address these issues, we propose Vector Optimization with Gaussian Process (VOGP), a probably approximately correct adaptive elimination algorithm that performs black-box vector optimization using Gaussian process bandits. VOGP allows users to convey objective preferences through ordering cones while performing efficient sampling by exploiting the smoothness of the objective function, resulting in a more effective optimization process that requires fewer evaluations. We establish theoretical guarantees for VOGP and derive information gain-based and kernel-specific sample complexity bounds. We also conduct experiments on both real-world and synthetic datasets to compare VOGP with the state-of-the-art methods.

Robust Bayesian Satisficing

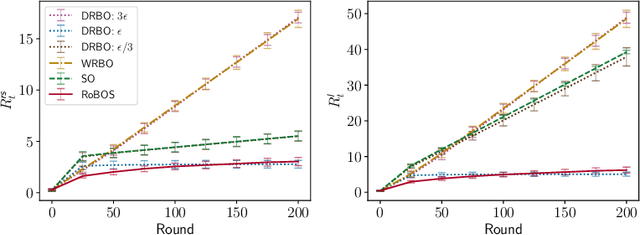
Distributional shifts pose a significant challenge to achieving robustness in contemporary machine learning. To overcome this challenge, robust satisficing (RS) seeks a robust solution to an unspecified distributional shift while achieving a utility above a desired threshold. This paper focuses on the problem of RS in contextual Bayesian optimization when there is a discrepancy between the true and reference distributions of the context. We propose a novel robust Bayesian satisficing algorithm called RoBOS for noisy black-box optimization. Our algorithm guarantees sublinear lenient regret under certain assumptions on the amount of distribution shift. In addition, we define a weaker notion of regret called robust satisficing regret, in which our algorithm achieves a sublinear upper bound independent of the amount of distribution shift. To demonstrate the effectiveness of our method, we apply it to various learning problems and compare it to other approaches, such as distributionally robust optimization.

Robust Pareto Set Identification with Contaminated Bandit Feedback

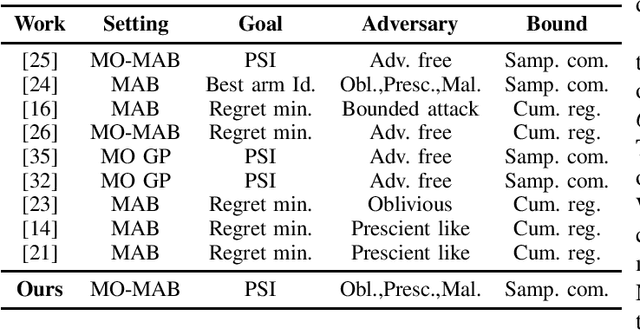
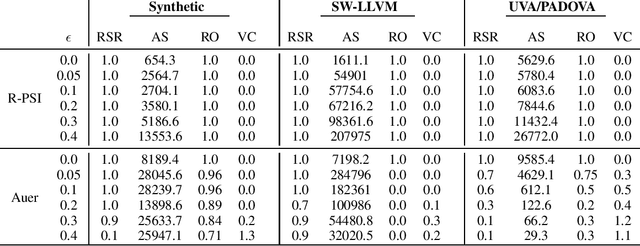
We consider the Pareto set identification (PSI) problem in multi-objective multi-armed bandits (MO-MAB) with contaminated reward observations. At each arm pull, with some probability, the true reward samples are replaced with the samples from an arbitrary contamination distribution chosen by the adversary. We propose a median-based MO-MAB algorithm for robust PSI that abides by the accuracy requirements set by the user via an accuracy parameter. We prove that the sample complexity of this algorithm depends on the accuracy parameter inverse squarely. We compare the proposed algorithm with a mean-based method from MO-MAB literature on Gaussian reward distributions. Our numerical results verify our theoretical expectations and show the necessity for robust algorithm design in the adversarial setting.

Federated Multi-Armed Bandits Under Byzantine Attacks

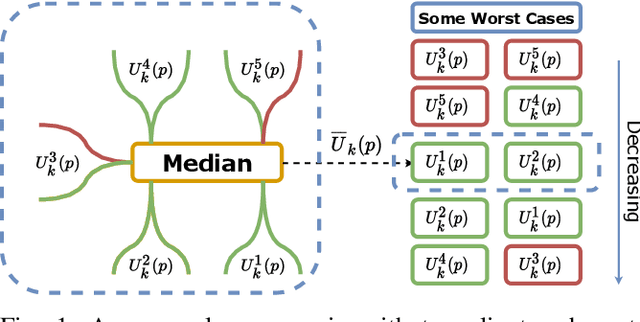
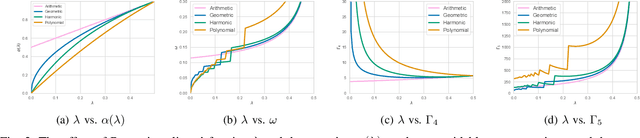
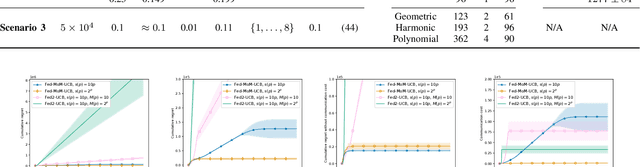
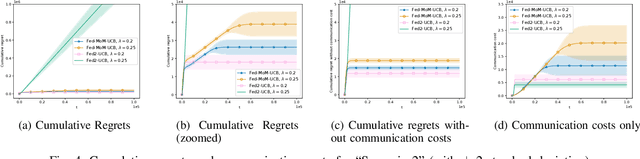
Multi-armed bandits (MAB) is a simple reinforcement learning model where the learner controls the trade-off between exploration versus exploitation to maximize its cumulative reward. Federated multi-armed bandits (FMAB) is a recently emerging framework where a cohort of learners with heterogeneous local models play a MAB game and communicate their aggregated feedback to a parameter server to learn the global feedback model. Federated learning models are vulnerable to adversarial attacks such as model-update attacks or data poisoning. In this work, we study an FMAB problem in the presence of Byzantine clients who can send false model updates that pose a threat to the learning process. We borrow tools from robust statistics and propose a median-of-means-based estimator: Fed-MoM-UCB, to cope with the Byzantine clients. We show that if the Byzantine clients constitute at most half the cohort, it is possible to incur a cumulative regret on the order of ${\cal O} (\log T)$ with respect to an unavoidable error margin, including the communication cost between the clients and the parameter server. We analyze the interplay between the algorithm parameters, unavoidable error margin, regret, communication cost, and the arms' suboptimality gaps. We demonstrate Fed-MoM-UCB's effectiveness against the baselines in the presence of Byzantine attacks via experiments.

Safe Linear Leveling Bandits

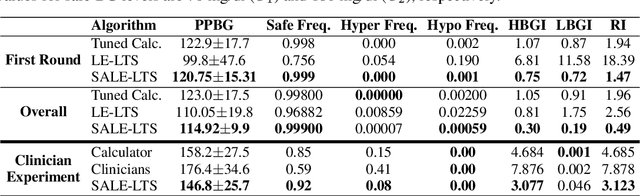
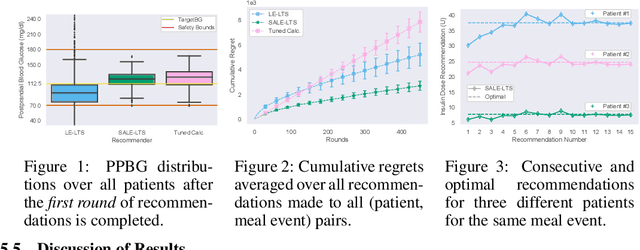
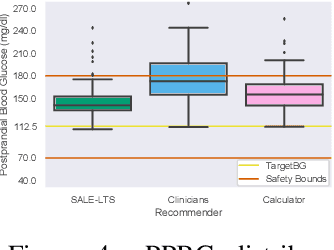
Multi-armed bandits (MAB) are extensively studied in various settings where the objective is to \textit{maximize} the actions' outcomes (i.e., rewards) over time. Since safety is crucial in many real-world problems, safe versions of MAB algorithms have also garnered considerable interest. In this work, we tackle a different critical task through the lens of \textit{linear stochastic bandits}, where the aim is to keep the actions' outcomes close to a target level while respecting a \textit{two-sided} safety constraint, which we call \textit{leveling}. Such a task is prevalent in numerous domains. Many healthcare problems, for instance, require keeping a physiological variable in a range and preferably close to a target level. The radical change in our objective necessitates a new acquisition strategy, which is at the heart of a MAB algorithm. We propose SALE-LTS: Safe Leveling via Linear Thompson Sampling algorithm, with a novel acquisition strategy to accommodate our task and show that it achieves sublinear regret with the same time and dimension dependence as previous works on the classical reward maximization problem absent any safety constraint. We demonstrate and discuss our algorithm's empirical performance in detail via thorough experiments.

Contextual Combinatorial Volatile Bandits with Satisfying via Gaussian Processes

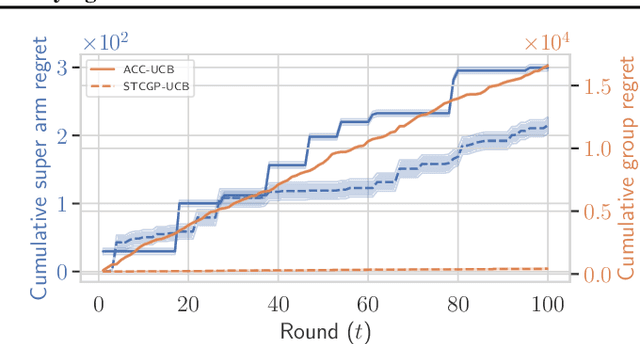
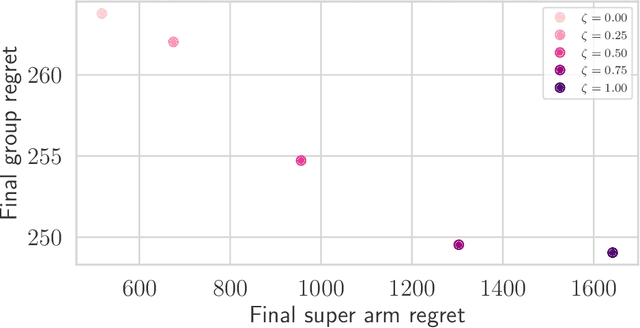
In many real-world applications of combinatorial bandits such as content caching, rewards must be maximized while satisfying minimum service requirements. In addition, base arm availabilities vary over time, and actions need to be adapted to the situation to maximize the rewards. We propose a new bandit model called Contextual Combinatorial Volatile Bandits with Group Thresholds to address these challenges. Our model subsumes combinatorial bandits by considering super arms to be subsets of groups of base arms. We seek to maximize super arm rewards while satisfying thresholds of all base arm groups that constitute a super arm. To this end, we define a new notion of regret that merges super arm reward maximization with group reward satisfaction. To facilitate learning, we assume that the mean outcomes of base arms are samples from a Gaussian Process indexed by the context set ${\cal X}$, and the expected reward is Lipschitz continuous in expected base arm outcomes. We propose an algorithm, called Thresholded Combinatorial Gaussian Process Upper Confidence Bounds (TCGP-UCB), that balances between maximizing cumulative reward and satisfying group reward thresholds and prove that it incurs $\tilde{O}(K\sqrt{T\overline{\gamma}_{T}} )$ regret with high probability, where $\overline{\gamma}_{T}$ is the maximum information gain associated with the set of base arm contexts that appeared in the first $T$ rounds and $K$ is the maximum super arm cardinality of any feasible action over all rounds. We show in experiments that our algorithm accumulates a reward comparable with that of the state-of-the-art combinatorial bandit algorithm while picking actions whose groups satisfy their thresholds.

ESCADA: Efficient Safety and Context Aware Dose Allocation for Precision Medicine

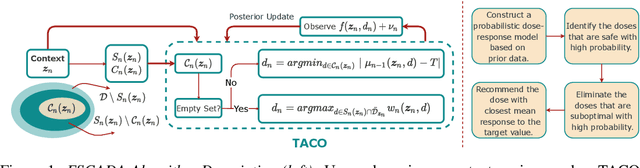
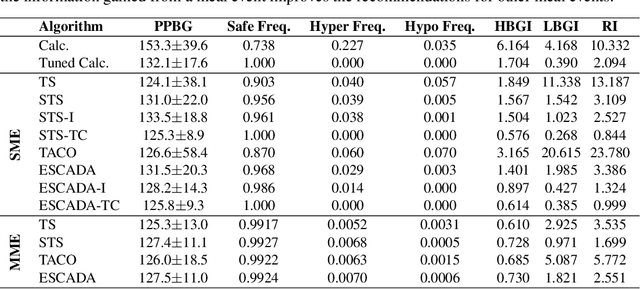
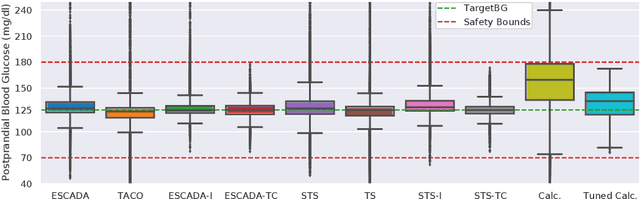
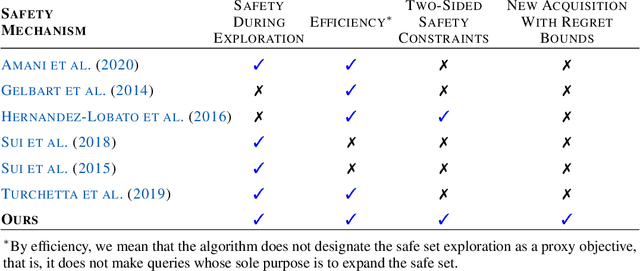
Finding an optimal individualized treatment regimen is considered one of the most challenging precision medicine problems. Various patient characteristics influence the response to the treatment, and hence, there is no one-size-fits-all regimen. Moreover, the administration of even a single unsafe dose during the treatment can have catastrophic consequences on patients' health. Therefore, an individualized treatment model must ensure patient {\em safety} while {\em efficiently} optimizing the course of therapy. In this work, we study a prevalent and essential medical problem setting where the treatment aims to keep a physiological variable in a range, preferably close to a target level. Such a task is relevant in numerous other domains as well. We propose ESCADA, a generic algorithm for this problem structure, to make individualized and context-aware optimal dose recommendations while assuring patient safety. We derive high probability upper bounds on the regret of ESCADA along with safety guarantees. Finally, we make extensive simulations on the {\em bolus insulin dose} allocation problem in type 1 diabetes mellitus disease and compare ESCADA's performance against Thompson sampling's, rule-based dose allocators', and clinicians'.

Vector Optimization with Stochastic Bandit Feedback

We introduce vector optimization problems with stochastic bandit feedback, which extends the best arm identification problem to vector-valued rewards. We consider $K$ designs, with multi-dimensional mean reward vectors, which are partially ordered according to a polyhedral ordering cone $C$. This generalizes the concept of Pareto set in multi-objective optimization and allows different sets of preferences of decision-makers to be encoded by $C$. Different than prior work, we define approximations of the Pareto set based on direction-free covering and gap notions. We study the setting where an evaluation of each design yields a noisy observation of the mean reward vector. Under subgaussian noise assumption, we investigate the sample complexity of the na\"ive elimination algorithm in an ($\epsilon,\delta$)-PAC setting, where the goal is to identify an ($\epsilon,\delta$)-PAC Pareto set with the minimum number of design evaluations. In particular, we identify cone-dependent geometric conditions on the deviations of empirical reward vectors from their mean under which the Pareto front can be approximated accurately. We run experiments to verify our theoretical results and illustrate how $C$ and sampling budget affect the Pareto set, returned ($\epsilon,\delta$)-PAC Pareto set and the success of identification.

Contextual Combinatorial Volatile Bandits via Gaussian Processes

We consider a contextual bandit problem with a combinatorial action set and time-varying base arm availability. At the beginning of each round, the agent observes the set of available base arms and their contexts and then selects an action that is a feasible subset of the set of available base arms to maximize its cumulative reward in the long run. We assume that the mean outcomes of base arms are samples from a Gaussian Process indexed by the context set ${\cal X}$, and the expected reward is Lipschitz continuous in expected base arm outcomes. For this setup, we propose an algorithm called Optimistic Combinatorial Learning and Optimization with Kernel Upper Confidence Bounds (O'CLOK-UCB) and prove that it incurs $\tilde{O}(K\sqrt{T\overline{\gamma}_{T}} )$ regret with high probability, where $\overline{\gamma}_{T}$ is the maximum information gain associated with the set of base arm contexts that appeared in the first $T$ rounds and $K$ is the maximum cardinality of any feasible action over all rounds. To dramatically speed up the algorithm, we also propose a variant of O'CLOK-UCB that uses sparse GPs. Finally, we experimentally show that both algorithms exploit inter-base arm outcome correlation and vastly outperform the previous state-of-the-art UCB-based algorithms in realistic setups.