Robust Pareto Set Identification with Contaminated Bandit Feedback

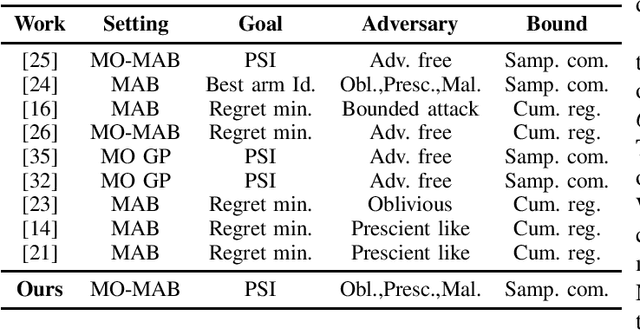
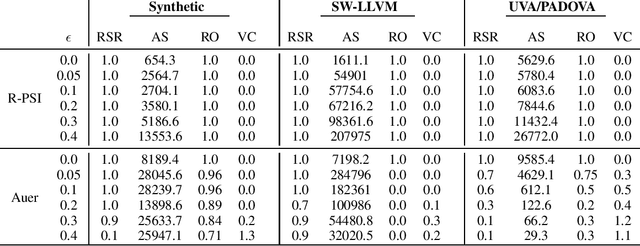
We consider the Pareto set identification (PSI) problem in multi-objective multi-armed bandits (MO-MAB) with contaminated reward observations. At each arm pull, with some probability, the true reward samples are replaced with the samples from an arbitrary contamination distribution chosen by the adversary. We propose a median-based MO-MAB algorithm for robust PSI that abides by the accuracy requirements set by the user via an accuracy parameter. We prove that the sample complexity of this algorithm depends on the accuracy parameter inverse squarely. We compare the proposed algorithm with a mean-based method from MO-MAB literature on Gaussian reward distributions. Our numerical results verify our theoretical expectations and show the necessity for robust algorithm design in the adversarial setting.

Pareto Active Learning with Gaussian Processes and Adaptive Discretization

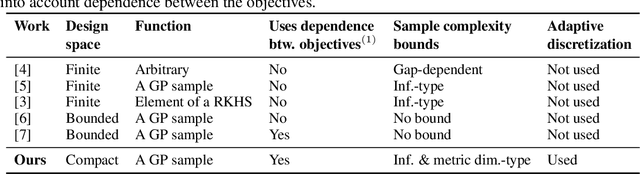
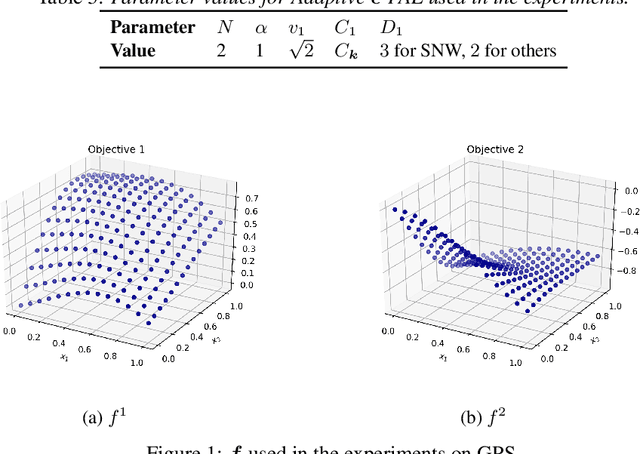
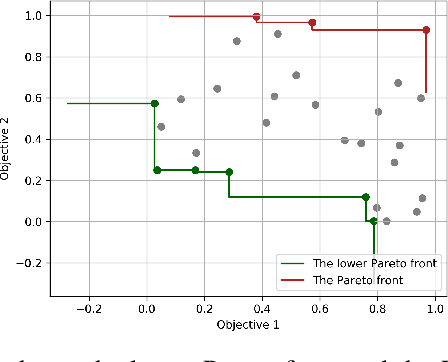
We consider the problem of optimizing a vector-valued objective function $\boldsymbol{f}$ sampled from a Gaussian Process (GP) whose index set is a well-behaved, compact metric space $({\cal X},d)$ of designs. We assume that $\boldsymbol{f}$ is not known beforehand and that evaluating $\boldsymbol{f}$ at design $x$ results in a noisy observation of $\boldsymbol{f}(x)$. Since identifying the Pareto optimal designs via exhaustive search is infeasible when the cardinality of ${\cal X}$ is large, we propose an algorithm, called Adaptive $\boldsymbol{\epsilon}$-PAL, that exploits the smoothness of the GP-sampled function and the structure of $({\cal X},d)$ to learn fast. In essence, Adaptive $\boldsymbol{\epsilon}$-PAL employs a tree-based adaptive discretization technique to identify an $\boldsymbol{\epsilon}$-accurate Pareto set of designs in as few evaluations as possible. We provide both information-type and metric dimension-type bounds on the sample complexity of $\boldsymbol{\epsilon}$-accurate Pareto set identification. We also experimentally show that our algorithm outperforms other Pareto set identification methods on several benchmark datasets.