Policy Teaching via Data Poisoning in Learning from Human Preferences

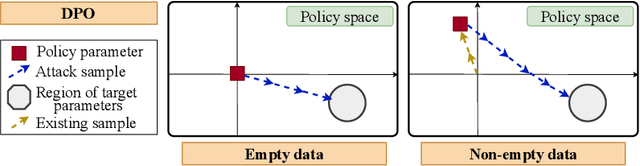
We study data poisoning attacks in learning from human preferences. More specifically, we consider the problem of teaching/enforcing a target policy $\pi^\dagger$ by synthesizing preference data. We seek to understand the susceptibility of different preference-based learning paradigms to poisoned preference data by analyzing the number of samples required by the attacker to enforce $\pi^\dagger$. We first propose a general data poisoning formulation in learning from human preferences and then study it for two popular paradigms, namely: (a) reinforcement learning from human feedback (RLHF) that operates by learning a reward model using preferences; (b) direct preference optimization (DPO) that directly optimizes policy using preferences. We conduct a theoretical analysis of the effectiveness of data poisoning in a setting where the attacker is allowed to augment a pre-existing dataset and also study its special case where the attacker can synthesize the entire preference dataset from scratch. As our main results, we provide lower/upper bounds on the number of samples required to enforce $\pi^\dagger$. Finally, we discuss the implications of our results in terms of the susceptibility of these learning paradigms under such data poisoning attacks.

Corruption-Robust Offline Two-Player Zero-Sum Markov Games

We study data corruption robustness in offline two-player zero-sum Markov games. Given a dataset of realized trajectories of two players, an adversary is allowed to modify an $\epsilon$-fraction of it. The learner's goal is to identify an approximate Nash Equilibrium policy pair from the corrupted data. We consider this problem in linear Markov games under different degrees of data coverage and corruption. We start by providing an information-theoretic lower bound on the suboptimality gap of any learner. Next, we propose robust versions of the Pessimistic Minimax Value Iteration algorithm, both under coverage on the corrupted data and under coverage only on the clean data, and show that they achieve (near)-optimal suboptimality gap bounds with respect to $\epsilon$. We note that we are the first to provide such a characterization of the problem of learning approximate Nash Equilibrium policies in offline two-player zero-sum Markov games under data corruption.

Reward Model Learning vs. Direct Policy Optimization: A Comparative Analysis of Learning from Human Preferences

In this paper, we take a step towards a deeper understanding of learning from human preferences by systematically comparing the paradigm of reinforcement learning from human feedback (RLHF) with the recently proposed paradigm of direct preference optimization (DPO). We focus our attention on the class of loglinear policy parametrization and linear reward functions. In order to compare the two paradigms, we first derive minimax statistical bounds on the suboptimality gap induced by both RLHF and DPO, assuming access to an oracle that exactly solves the optimization problems. We provide a detailed discussion on the relative comparison between the two paradigms, simultaneously taking into account the sample size, policy and reward class dimensions, and the regularization temperature. Moreover, we extend our analysis to the approximate optimization setting and derive exponentially decaying convergence rates for both RLHF and DPO. Next, we analyze the setting where the ground-truth reward is not realizable and find that, while RLHF incurs a constant additional error, DPO retains its asymptotically decaying gap by just tuning the temperature accordingly. Finally, we extend our comparison to the Markov decision process setting, where we generalize our results with exact optimization. To the best of our knowledge, we are the first to provide such a comparative analysis for RLHF and DPO.

Corruption Robust Offline Reinforcement Learning with Human Feedback

We study data corruption robustness for reinforcement learning with human feedback (RLHF) in an offline setting. Given an offline dataset of pairs of trajectories along with feedback about human preferences, an $\varepsilon$-fraction of the pairs is corrupted (e.g., feedback flipped or trajectory features manipulated), capturing an adversarial attack or noisy human preferences. We aim to design algorithms that identify a near-optimal policy from the corrupted data, with provable guarantees. Existing theoretical works have separately studied the settings of corruption robust RL (learning from scalar rewards directly under corruption) and offline RLHF (learning from human feedback without corruption); however, they are inapplicable to our problem of dealing with corrupted data in offline RLHF setting. To this end, we design novel corruption robust offline RLHF methods under various assumptions on the coverage of the data-generating distributions. At a high level, our methodology robustifies an offline RLHF framework by first learning a reward model along with confidence sets and then learning a pessimistic optimal policy over the confidence set. Our key insight is that learning optimal policy can be done by leveraging an offline corruption-robust RL oracle in different ways (e.g., zero-order oracle or first-order oracle), depending on the data coverage assumptions. To our knowledge, ours is the first work that provides provable corruption robust offline RLHF methods.

Contextual Combinatorial Volatile Bandits via Gaussian Processes

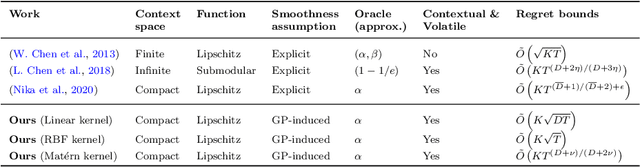
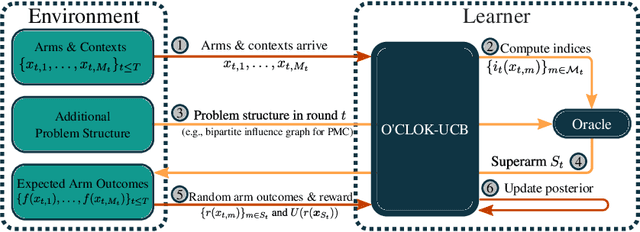
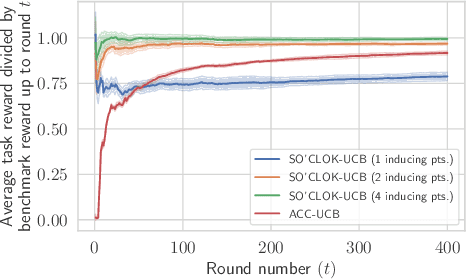
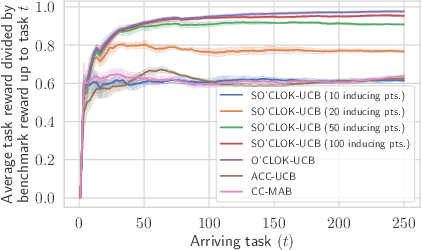
We consider a contextual bandit problem with a combinatorial action set and time-varying base arm availability. At the beginning of each round, the agent observes the set of available base arms and their contexts and then selects an action that is a feasible subset of the set of available base arms to maximize its cumulative reward in the long run. We assume that the mean outcomes of base arms are samples from a Gaussian Process indexed by the context set ${\cal X}$, and the expected reward is Lipschitz continuous in expected base arm outcomes. For this setup, we propose an algorithm called Optimistic Combinatorial Learning and Optimization with Kernel Upper Confidence Bounds (O'CLOK-UCB) and prove that it incurs $\tilde{O}(K\sqrt{T\overline{\gamma}_{T}} )$ regret with high probability, where $\overline{\gamma}_{T}$ is the maximum information gain associated with the set of base arm contexts that appeared in the first $T$ rounds and $K$ is the maximum cardinality of any feasible action over all rounds. To dramatically speed up the algorithm, we also propose a variant of O'CLOK-UCB that uses sparse GPs. Finally, we experimentally show that both algorithms exploit inter-base arm outcome correlation and vastly outperform the previous state-of-the-art UCB-based algorithms in realistic setups.

Pareto Active Learning with Gaussian Processes and Adaptive Discretization

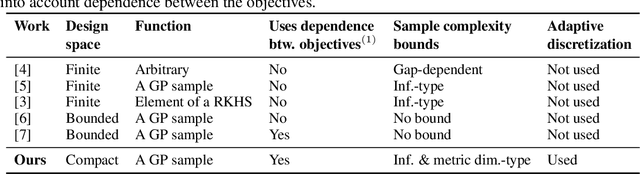
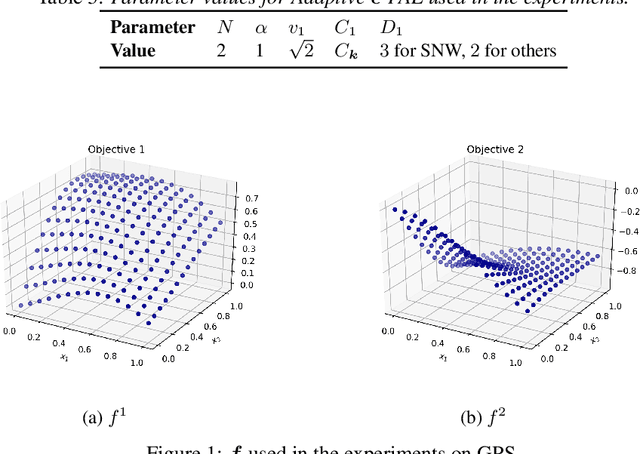
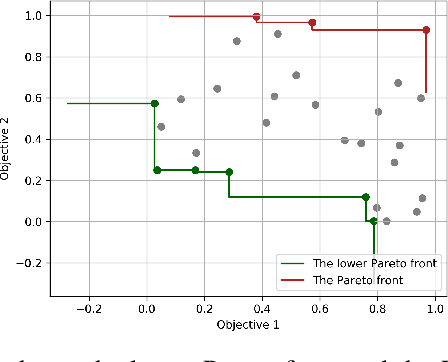
We consider the problem of optimizing a vector-valued objective function $\boldsymbol{f}$ sampled from a Gaussian Process (GP) whose index set is a well-behaved, compact metric space $({\cal X},d)$ of designs. We assume that $\boldsymbol{f}$ is not known beforehand and that evaluating $\boldsymbol{f}$ at design $x$ results in a noisy observation of $\boldsymbol{f}(x)$. Since identifying the Pareto optimal designs via exhaustive search is infeasible when the cardinality of ${\cal X}$ is large, we propose an algorithm, called Adaptive $\boldsymbol{\epsilon}$-PAL, that exploits the smoothness of the GP-sampled function and the structure of $({\cal X},d)$ to learn fast. In essence, Adaptive $\boldsymbol{\epsilon}$-PAL employs a tree-based adaptive discretization technique to identify an $\boldsymbol{\epsilon}$-accurate Pareto set of designs in as few evaluations as possible. We provide both information-type and metric dimension-type bounds on the sample complexity of $\boldsymbol{\epsilon}$-accurate Pareto set identification. We also experimentally show that our algorithm outperforms other Pareto set identification methods on several benchmark datasets.