Pareto Active Learning with Gaussian Processes and Adaptive Discretization
Paper and Code
Jun 24, 2020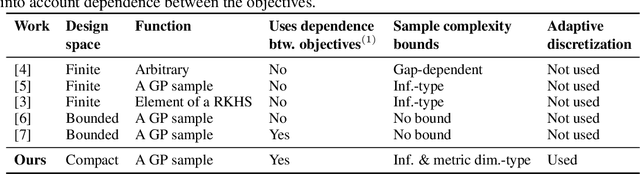
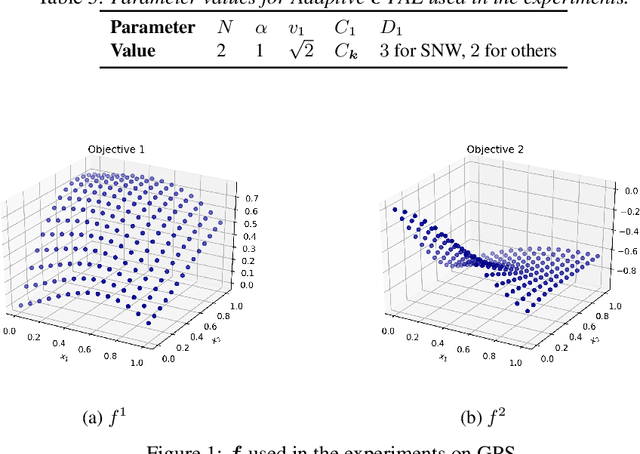

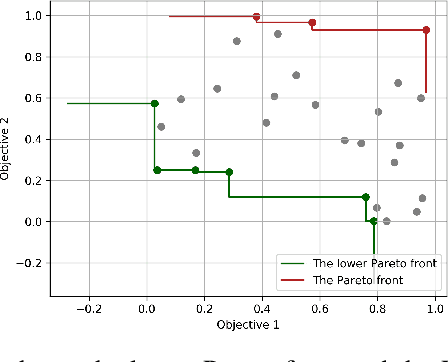
We consider the problem of optimizing a vector-valued objective function $\boldsymbol{f}$ sampled from a Gaussian Process (GP) whose index set is a well-behaved, compact metric space $({\cal X},d)$ of designs. We assume that $\boldsymbol{f}$ is not known beforehand and that evaluating $\boldsymbol{f}$ at design $x$ results in a noisy observation of $\boldsymbol{f}(x)$. Since identifying the Pareto optimal designs via exhaustive search is infeasible when the cardinality of ${\cal X}$ is large, we propose an algorithm, called Adaptive $\boldsymbol{\epsilon}$-PAL, that exploits the smoothness of the GP-sampled function and the structure of $({\cal X},d)$ to learn fast. In essence, Adaptive $\boldsymbol{\epsilon}$-PAL employs a tree-based adaptive discretization technique to identify an $\boldsymbol{\epsilon}$-accurate Pareto set of designs in as few evaluations as possible. We provide both information-type and metric dimension-type bounds on the sample complexity of $\boldsymbol{\epsilon}$-accurate Pareto set identification. We also experimentally show that our algorithm outperforms other Pareto set identification methods on several benchmark datasets.
 Add to Chrome
Add to Chrome Add to Firefox
Add to Firefox Add to Edge
Add to Edge