VOPy: A Framework for Black-box Vector Optimization

We introduce VOPy, an open-source Python library designed to address black-box vector optimization, where multiple objectives must be optimized simultaneously with respect to a partial order induced by a convex cone. VOPy extends beyond traditional multi-objective optimization (MOO) tools by enabling flexible, cone-based ordering of solutions; with an application scope that includes environments with observation noise, discrete or continuous design spaces, limited budgets, and batch observations. VOPy provides a modular architecture, facilitating the integration of existing methods and the development of novel algorithms. We detail VOPy's architecture, usage, and potential to advance research and application in the field of vector optimization. The source code for VOPy is available at https://github.com/Bilkent-CYBORG/VOPy.

Vector Optimization with Gaussian Process Bandits

Learning problems in which multiple conflicting objectives must be considered simultaneously often arise in various fields, including engineering, drug design, and environmental management. Traditional methods for dealing with multiple black-box objective functions, such as scalarization and identification of the Pareto set under the componentwise order, have limitations in incorporating objective preferences and exploring the solution space accordingly. While vector optimization offers improved flexibility and adaptability via specifying partial orders based on ordering cones, current techniques designed for sequential experiments either suffer from high sample complexity or lack theoretical guarantees. To address these issues, we propose Vector Optimization with Gaussian Process (VOGP), a probably approximately correct adaptive elimination algorithm that performs black-box vector optimization using Gaussian process bandits. VOGP allows users to convey objective preferences through ordering cones while performing efficient sampling by exploiting the smoothness of the objective function, resulting in a more effective optimization process that requires fewer evaluations. We establish theoretical guarantees for VOGP and derive information gain-based and kernel-specific sample complexity bounds. We also conduct experiments on both real-world and synthetic datasets to compare VOGP with the state-of-the-art methods.

Vector Optimization with Stochastic Bandit Feedback

We introduce vector optimization problems with stochastic bandit feedback, which extends the best arm identification problem to vector-valued rewards. We consider $K$ designs, with multi-dimensional mean reward vectors, which are partially ordered according to a polyhedral ordering cone $C$. This generalizes the concept of Pareto set in multi-objective optimization and allows different sets of preferences of decision-makers to be encoded by $C$. Different than prior work, we define approximations of the Pareto set based on direction-free covering and gap notions. We study the setting where an evaluation of each design yields a noisy observation of the mean reward vector. Under subgaussian noise assumption, we investigate the sample complexity of the na\"ive elimination algorithm in an ($\epsilon,\delta$)-PAC setting, where the goal is to identify an ($\epsilon,\delta$)-PAC Pareto set with the minimum number of design evaluations. In particular, we identify cone-dependent geometric conditions on the deviations of empirical reward vectors from their mean under which the Pareto front can be approximated accurately. We run experiments to verify our theoretical results and illustrate how $C$ and sampling budget affect the Pareto set, returned ($\epsilon,\delta$)-PAC Pareto set and the success of identification.

Pareto Active Learning with Gaussian Processes and Adaptive Discretization

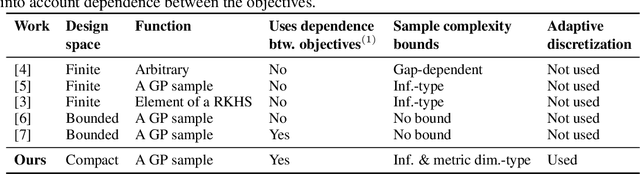
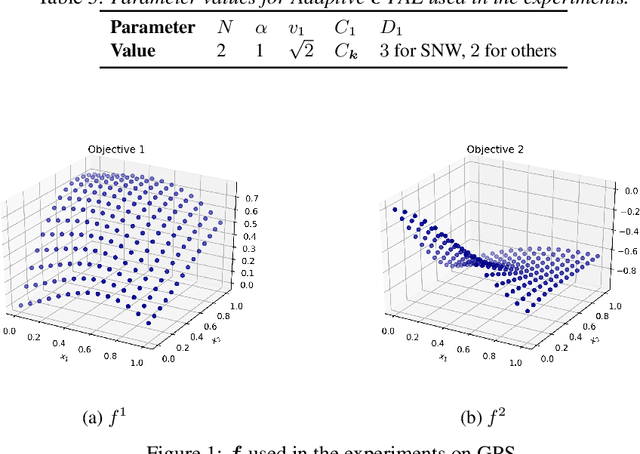
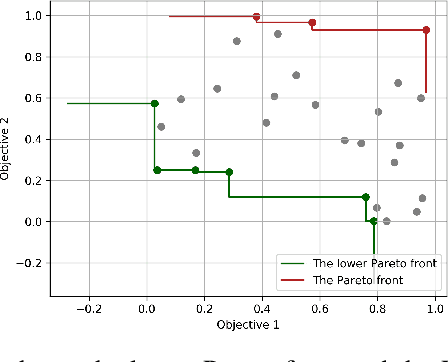
We consider the problem of optimizing a vector-valued objective function $\boldsymbol{f}$ sampled from a Gaussian Process (GP) whose index set is a well-behaved, compact metric space $({\cal X},d)$ of designs. We assume that $\boldsymbol{f}$ is not known beforehand and that evaluating $\boldsymbol{f}$ at design $x$ results in a noisy observation of $\boldsymbol{f}(x)$. Since identifying the Pareto optimal designs via exhaustive search is infeasible when the cardinality of ${\cal X}$ is large, we propose an algorithm, called Adaptive $\boldsymbol{\epsilon}$-PAL, that exploits the smoothness of the GP-sampled function and the structure of $({\cal X},d)$ to learn fast. In essence, Adaptive $\boldsymbol{\epsilon}$-PAL employs a tree-based adaptive discretization technique to identify an $\boldsymbol{\epsilon}$-accurate Pareto set of designs in as few evaluations as possible. We provide both information-type and metric dimension-type bounds on the sample complexity of $\boldsymbol{\epsilon}$-accurate Pareto set identification. We also experimentally show that our algorithm outperforms other Pareto set identification methods on several benchmark datasets.