Yaşar Cahit Yıldırım
VOPy: A Framework for Black-box Vector Optimization
Dec 09, 2024Abstract:We introduce VOPy, an open-source Python library designed to address black-box vector optimization, where multiple objectives must be optimized simultaneously with respect to a partial order induced by a convex cone. VOPy extends beyond traditional multi-objective optimization (MOO) tools by enabling flexible, cone-based ordering of solutions; with an application scope that includes environments with observation noise, discrete or continuous design spaces, limited budgets, and batch observations. VOPy provides a modular architecture, facilitating the integration of existing methods and the development of novel algorithms. We detail VOPy's architecture, usage, and potential to advance research and application in the field of vector optimization. The source code for VOPy is available at https://github.com/Bilkent-CYBORG/VOPy.
Vector Optimization with Gaussian Process Bandits
Dec 03, 2024Abstract:Learning problems in which multiple conflicting objectives must be considered simultaneously often arise in various fields, including engineering, drug design, and environmental management. Traditional methods for dealing with multiple black-box objective functions, such as scalarization and identification of the Pareto set under the componentwise order, have limitations in incorporating objective preferences and exploring the solution space accordingly. While vector optimization offers improved flexibility and adaptability via specifying partial orders based on ordering cones, current techniques designed for sequential experiments either suffer from high sample complexity or lack theoretical guarantees. To address these issues, we propose Vector Optimization with Gaussian Process (VOGP), a probably approximately correct adaptive elimination algorithm that performs black-box vector optimization using Gaussian process bandits. VOGP allows users to convey objective preferences through ordering cones while performing efficient sampling by exploiting the smoothness of the objective function, resulting in a more effective optimization process that requires fewer evaluations. We establish theoretical guarantees for VOGP and derive information gain-based and kernel-specific sample complexity bounds. We also conduct experiments on both real-world and synthetic datasets to compare VOGP with the state-of-the-art methods.
Robust Bayesian Satisficing
Aug 16, 2023

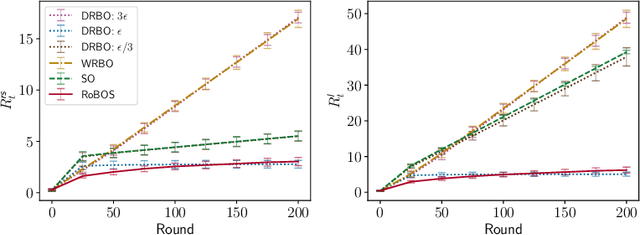

Abstract:Distributional shifts pose a significant challenge to achieving robustness in contemporary machine learning. To overcome this challenge, robust satisficing (RS) seeks a robust solution to an unspecified distributional shift while achieving a utility above a desired threshold. This paper focuses on the problem of RS in contextual Bayesian optimization when there is a discrepancy between the true and reference distributions of the context. We propose a novel robust Bayesian satisficing algorithm called RoBOS for noisy black-box optimization. Our algorithm guarantees sublinear lenient regret under certain assumptions on the amount of distribution shift. In addition, we define a weaker notion of regret called robust satisficing regret, in which our algorithm achieves a sublinear upper bound independent of the amount of distribution shift. To demonstrate the effectiveness of our method, we apply it to various learning problems and compare it to other approaches, such as distributionally robust optimization.
 Add to Chrome
Add to Chrome Add to Firefox
Add to Firefox Add to Edge
Add to Edge