Can In-Context Reinforcement Learning Recover From Reward Poisoning Attacks?

We study the corruption-robustness of in-context reinforcement learning (ICRL), focusing on the Decision-Pretrained Transformer (DPT, Lee et al., 2023). To address the challenge of reward poisoning attacks targeting the DPT, we propose a novel adversarial training framework, called Adversarially Trained Decision-Pretrained Transformer (AT-DPT). Our method simultaneously trains an attacker to minimize the true reward of the DPT by poisoning environment rewards, and a DPT model to infer optimal actions from the poisoned data. We evaluate the effectiveness of our approach against standard bandit algorithms, including robust baselines designed to handle reward contamination. Our results show that the proposed method significantly outperforms these baselines in bandit settings, under a learned attacker. We additionally evaluate AT-DPT on an adaptive attacker, and observe similar results. Furthermore, we extend our evaluation to the MDP setting, confirming that the robustness observed in bandit scenarios generalizes to more complex environments.

Independent Learning in Performative Markov Potential Games

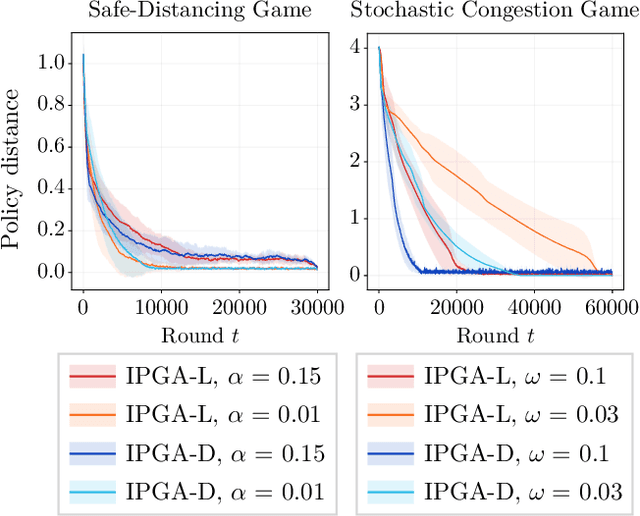
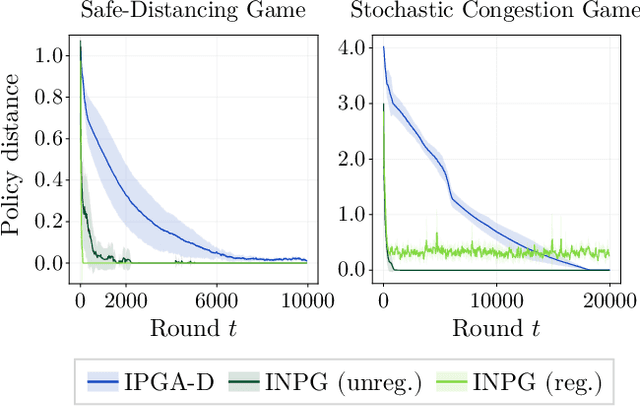
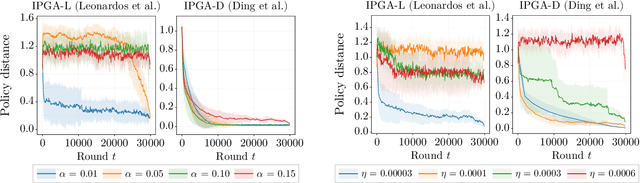
Performative Reinforcement Learning (PRL) refers to a scenario in which the deployed policy changes the reward and transition dynamics of the underlying environment. In this work, we study multi-agent PRL by incorporating performative effects into Markov Potential Games (MPGs). We introduce the notion of a performatively stable equilibrium (PSE) and show that it always exists under a reasonable sensitivity assumption. We then provide convergence results for state-of-the-art algorithms used to solve MPGs. Specifically, we show that independent policy gradient ascent (IPGA) and independent natural policy gradient (INPG) converge to an approximate PSE in the best-iterate sense, with an additional term that accounts for the performative effects. Furthermore, we show that INPG asymptotically converges to a PSE in the last-iterate sense. As the performative effects vanish, we recover the convergence rates from prior work. For a special case of our game, we provide finite-time last-iterate convergence results for a repeated retraining approach, in which agents independently optimize a surrogate objective. We conduct extensive experiments to validate our theoretical findings.

Policy Teaching via Data Poisoning in Learning from Human Preferences

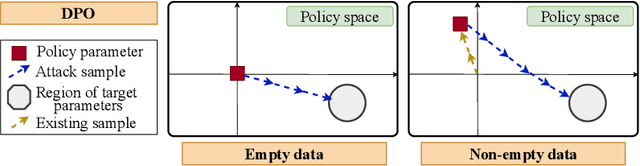
We study data poisoning attacks in learning from human preferences. More specifically, we consider the problem of teaching/enforcing a target policy $\pi^\dagger$ by synthesizing preference data. We seek to understand the susceptibility of different preference-based learning paradigms to poisoned preference data by analyzing the number of samples required by the attacker to enforce $\pi^\dagger$. We first propose a general data poisoning formulation in learning from human preferences and then study it for two popular paradigms, namely: (a) reinforcement learning from human feedback (RLHF) that operates by learning a reward model using preferences; (b) direct preference optimization (DPO) that directly optimizes policy using preferences. We conduct a theoretical analysis of the effectiveness of data poisoning in a setting where the attacker is allowed to augment a pre-existing dataset and also study its special case where the attacker can synthesize the entire preference dataset from scratch. As our main results, we provide lower/upper bounds on the number of samples required to enforce $\pi^\dagger$. Finally, we discuss the implications of our results in terms of the susceptibility of these learning paradigms under such data poisoning attacks.

Text-Diffusion Red-Teaming of Large Language Models: Unveiling Harmful Behaviors with Proximity Constraints

Recent work has proposed automated red-teaming methods for testing the vulnerabilities of a given target large language model (LLM). These methods use red-teaming LLMs to uncover inputs that induce harmful behavior in a target LLM. In this paper, we study red-teaming strategies that enable a targeted security assessment. We propose an optimization framework for red-teaming with proximity constraints, where the discovered prompts must be similar to reference prompts from a given dataset. This dataset serves as a template for the discovered prompts, anchoring the search for test-cases to specific topics, writing styles, or types of harmful behavior. We show that established auto-regressive model architectures do not perform well in this setting. We therefore introduce a black-box red-teaming method inspired by text-diffusion models: Diffusion for Auditing and Red-Teaming (DART). DART modifies the reference prompt by perturbing it in the embedding space, directly controlling the amount of change introduced. We systematically evaluate our method by comparing its effectiveness with established methods based on model fine-tuning and zero- and few-shot prompting. Our results show that DART is significantly more effective at discovering harmful inputs in close proximity to the reference prompt.

Corruption-Robust Offline Two-Player Zero-Sum Markov Games

We study data corruption robustness in offline two-player zero-sum Markov games. Given a dataset of realized trajectories of two players, an adversary is allowed to modify an $\epsilon$-fraction of it. The learner's goal is to identify an approximate Nash Equilibrium policy pair from the corrupted data. We consider this problem in linear Markov games under different degrees of data coverage and corruption. We start by providing an information-theoretic lower bound on the suboptimality gap of any learner. Next, we propose robust versions of the Pessimistic Minimax Value Iteration algorithm, both under coverage on the corrupted data and under coverage only on the clean data, and show that they achieve (near)-optimal suboptimality gap bounds with respect to $\epsilon$. We note that we are the first to provide such a characterization of the problem of learning approximate Nash Equilibrium policies in offline two-player zero-sum Markov games under data corruption.

Reward Model Learning vs. Direct Policy Optimization: A Comparative Analysis of Learning from Human Preferences

In this paper, we take a step towards a deeper understanding of learning from human preferences by systematically comparing the paradigm of reinforcement learning from human feedback (RLHF) with the recently proposed paradigm of direct preference optimization (DPO). We focus our attention on the class of loglinear policy parametrization and linear reward functions. In order to compare the two paradigms, we first derive minimax statistical bounds on the suboptimality gap induced by both RLHF and DPO, assuming access to an oracle that exactly solves the optimization problems. We provide a detailed discussion on the relative comparison between the two paradigms, simultaneously taking into account the sample size, policy and reward class dimensions, and the regularization temperature. Moreover, we extend our analysis to the approximate optimization setting and derive exponentially decaying convergence rates for both RLHF and DPO. Next, we analyze the setting where the ground-truth reward is not realizable and find that, while RLHF incurs a constant additional error, DPO retains its asymptotically decaying gap by just tuning the temperature accordingly. Finally, we extend our comparison to the Markov decision process setting, where we generalize our results with exact optimization. To the best of our knowledge, we are the first to provide such a comparative analysis for RLHF and DPO.

Corruption Robust Offline Reinforcement Learning with Human Feedback

We study data corruption robustness for reinforcement learning with human feedback (RLHF) in an offline setting. Given an offline dataset of pairs of trajectories along with feedback about human preferences, an $\varepsilon$-fraction of the pairs is corrupted (e.g., feedback flipped or trajectory features manipulated), capturing an adversarial attack or noisy human preferences. We aim to design algorithms that identify a near-optimal policy from the corrupted data, with provable guarantees. Existing theoretical works have separately studied the settings of corruption robust RL (learning from scalar rewards directly under corruption) and offline RLHF (learning from human feedback without corruption); however, they are inapplicable to our problem of dealing with corrupted data in offline RLHF setting. To this end, we design novel corruption robust offline RLHF methods under various assumptions on the coverage of the data-generating distributions. At a high level, our methodology robustifies an offline RLHF framework by first learning a reward model along with confidence sets and then learning a pessimistic optimal policy over the confidence set. Our key insight is that learning optimal policy can be done by leveraging an offline corruption-robust RL oracle in different ways (e.g., zero-order oracle or first-order oracle), depending on the data coverage assumptions. To our knowledge, ours is the first work that provides provable corruption robust offline RLHF methods.