Neural Bandit Based Optimal LLM Selection for a Pipeline of Tasks

With the increasing popularity of large language models (LLMs) for a variety of tasks, there has been a growing interest in strategies that can predict which out of a set of LLMs will yield a successful answer at low cost. This problem promises to become more and more relevant as providers like Microsoft allow users to easily create custom LLM "assistants" specialized to particular types of queries. However, some tasks (i.e., queries) may be too specialized and difficult for a single LLM to handle alone. These applications often benefit from breaking down the task into smaller subtasks, each of which can then be executed by a LLM expected to perform well on that specific subtask. For example, in extracting a diagnosis from medical records, one can first select an LLM to summarize the record, select another to validate the summary, and then select another, possibly different, LLM to extract the diagnosis from the summarized record. Unlike existing LLM selection or routing algorithms, this setting requires that we select a sequence of LLMs, with the output of each LLM feeding into the next and potentially influencing its success. Thus, unlike single LLM selection, the quality of each subtask's output directly affects the inputs, and hence the cost and success rate, of downstream LLMs, creating complex performance dependencies that must be learned and accounted for during selection. We propose a neural contextual bandit-based algorithm that trains neural networks that model LLM success on each subtask in an online manner, thus learning to guide the LLM selections for the different subtasks, even in the absence of historical LLM performance data. Experiments on telecommunications question answering and medical diagnosis prediction datasets illustrate the effectiveness of our proposed approach compared to other LLM selection algorithms.

Semantic Caching for Low-Cost LLM Serving: From Offline Learning to Online Adaptation

Large Language Models (LLMs) are revolutionizing how users interact with information systems, yet their high inference cost poses serious scalability and sustainability challenges. Caching inference responses, allowing them to be retrieved without another forward pass through the LLM, has emerged as one possible solution. Traditional exact-match caching, however, overlooks the semantic similarity between queries, leading to unnecessary recomputation. Semantic caching addresses this by retrieving responses based on semantic similarity, but introduces a fundamentally different cache eviction problem: one must account for mismatch costs between incoming queries and cached responses. Moreover, key system parameters, such as query arrival probabilities and serving costs, are often unknown and must be learned over time. Existing semantic caching methods are largely ad-hoc, lacking theoretical foundations and unable to adapt to real-world uncertainty. In this paper, we present a principled, learning-based framework for semantic cache eviction under unknown query and cost distributions. We formulate both offline optimization and online learning variants of the problem, and develop provably efficient algorithms with state-of-the-art guarantees. We also evaluate our framework on a synthetic dataset, showing that our proposed algorithms perform matching or superior performance compared with baselines.

Neural Combinatorial Clustered Bandits for Recommendation Systems

We consider the contextual combinatorial bandit setting where in each round, the learning agent, e.g., a recommender system, selects a subset of "arms," e.g., products, and observes rewards for both the individual base arms, which are a function of known features (called "context"), and the super arm (the subset of arms), which is a function of the base arm rewards. The agent's goal is to simultaneously learn the unknown reward functions and choose the highest-reward arms. For example, the "reward" may represent a user's probability of clicking on one of the recommended products. Conventional bandit models, however, employ restrictive reward function models in order to obtain performance guarantees. We make use of deep neural networks to estimate and learn the unknown reward functions and propose Neural UCB Clustering (NeUClust), which adopts a clustering approach to select the super arm in every round by exploiting underlying structure in the context space. Unlike prior neural bandit works, NeUClust uses a neural network to estimate the super arm reward and select the super arm, thus eliminating the need for a known optimization oracle. We non-trivially extend prior neural combinatorial bandit works to prove that NeUClust achieves $\widetilde{O}\left(\widetilde{d}\sqrt{T}\right)$ regret, where $\widetilde{d}$ is the effective dimension of a neural tangent kernel matrix, $T$ the number of rounds. Experiments on real world recommendation datasets show that NeUClust achieves better regret and reward than other contextual combinatorial and neural bandit algorithms.

Contextual Combinatorial Volatile Bandits with Satisfying via Gaussian Processes

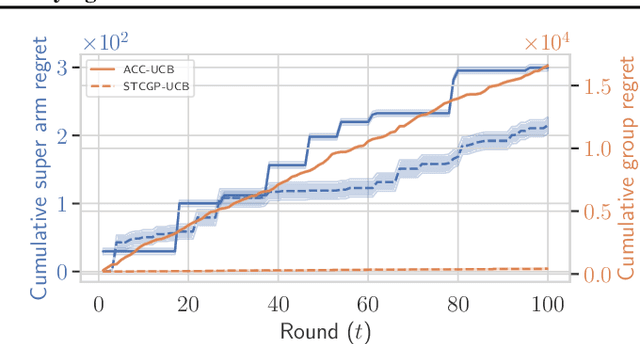
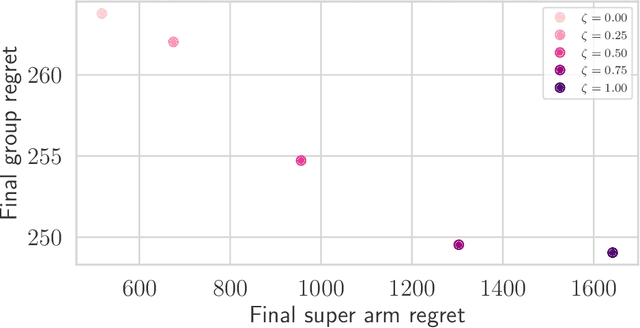
In many real-world applications of combinatorial bandits such as content caching, rewards must be maximized while satisfying minimum service requirements. In addition, base arm availabilities vary over time, and actions need to be adapted to the situation to maximize the rewards. We propose a new bandit model called Contextual Combinatorial Volatile Bandits with Group Thresholds to address these challenges. Our model subsumes combinatorial bandits by considering super arms to be subsets of groups of base arms. We seek to maximize super arm rewards while satisfying thresholds of all base arm groups that constitute a super arm. To this end, we define a new notion of regret that merges super arm reward maximization with group reward satisfaction. To facilitate learning, we assume that the mean outcomes of base arms are samples from a Gaussian Process indexed by the context set ${\cal X}$, and the expected reward is Lipschitz continuous in expected base arm outcomes. We propose an algorithm, called Thresholded Combinatorial Gaussian Process Upper Confidence Bounds (TCGP-UCB), that balances between maximizing cumulative reward and satisfying group reward thresholds and prove that it incurs $\tilde{O}(K\sqrt{T\overline{\gamma}_{T}} )$ regret with high probability, where $\overline{\gamma}_{T}$ is the maximum information gain associated with the set of base arm contexts that appeared in the first $T$ rounds and $K$ is the maximum super arm cardinality of any feasible action over all rounds. We show in experiments that our algorithm accumulates a reward comparable with that of the state-of-the-art combinatorial bandit algorithm while picking actions whose groups satisfy their thresholds.