Doubly robust identification of treatment effects from multiple environments

Practical and ethical constraints often require the use of observational data for causal inference, particularly in medicine and social sciences. Yet, observational datasets are prone to confounding, potentially compromising the validity of causal conclusions. While it is possible to correct for biases if the underlying causal graph is known, this is rarely a feasible ask in practical scenarios. A common strategy is to adjust for all available covariates, yet this approach can yield biased treatment effect estimates, especially when post-treatment or unobserved variables are present. We propose RAMEN, an algorithm that produces unbiased treatment effect estimates by leveraging the heterogeneity of multiple data sources without the need to know or learn the underlying causal graph. Notably, RAMEN achieves doubly robust identification: it can identify the treatment effect whenever the causal parents of the treatment or those of the outcome are observed, and the node whose parents are observed satisfies an invariance assumption. Empirical evaluations on synthetic and real-world datasets show that our approach outperforms existing methods.

Causal Lifting of Neural Representations: Zero-Shot Generalization for Causal Inferences

A plethora of real-world scientific investigations is waiting to scale with the support of trustworthy predictive models that can reduce the need for costly data annotations. We focus on causal inferences on a target experiment with unlabeled factual outcomes, retrieved by a predictive model fine-tuned on a labeled similar experiment. First, we show that factual outcome estimation via Empirical Risk Minimization (ERM) may fail to yield valid causal inferences on the target population, even in a randomized controlled experiment and infinite training samples. Then, we propose to leverage the observed experimental settings during training to empower generalization to downstream interventional investigations, ``Causal Lifting'' the predictive model. We propose Deconfounded Empirical Risk Minimization (DERM), a new simple learning procedure minimizing the risk over a fictitious target population, preventing potential confounding effects. We validate our method on both synthetic and real-world scientific data. Notably, for the first time, we zero-shot generalize causal inferences on ISTAnt dataset (without annotation) by causal lifting a predictive model on our experiment variant.

Efficient Randomized Experiments Using Foundation Models

Randomized experiments are the preferred approach for evaluating the effects of interventions, but they are costly and often yield estimates with substantial uncertainty. On the other hand, in silico experiments leveraging foundation models offer a cost-effective alternative that can potentially attain higher statistical precision. However, the benefits of in silico experiments come with a significant risk: statistical inferences are not valid if the models fail to accurately predict experimental responses to interventions. In this paper, we propose a novel approach that integrates the predictions from multiple foundation models with experimental data while preserving valid statistical inference. Our estimator is consistent and asymptotically normal, with asymptotic variance no larger than the standard estimator based on experimental data alone. Importantly, these statistical properties hold even when model predictions are arbitrarily biased. Empirical results across several randomized experiments show that our estimator offers substantial precision gains, equivalent to a reduction of up to 20% in the sample size needed to match the same precision as the standard estimator based on experimental data alone.

Detecting critical treatment effect bias in small subgroups

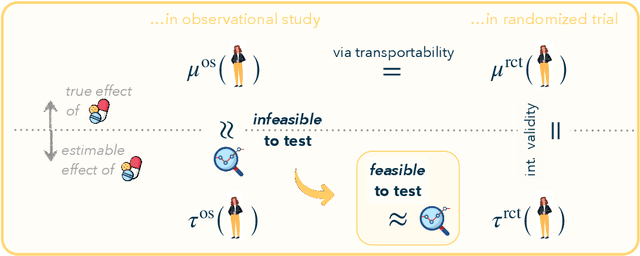
Randomized trials are considered the gold standard for making informed decisions in medicine, yet they often lack generalizability to the patient populations in clinical practice. Observational studies, on the other hand, cover a broader patient population but are prone to various biases. Thus, before using an observational study for decision-making, it is crucial to benchmark its treatment effect estimates against those derived from a randomized trial. We propose a novel strategy to benchmark observational studies beyond the average treatment effect. First, we design a statistical test for the null hypothesis that the treatment effects estimated from the two studies, conditioned on a set of relevant features, differ up to some tolerance. We then estimate an asymptotically valid lower bound on the maximum bias strength for any subgroup in the observational study. Finally, we validate our benchmarking strategy in a real-world setting and show that it leads to conclusions that align with established medical knowledge.

Hidden yet quantifiable: A lower bound for confounding strength using randomized trials

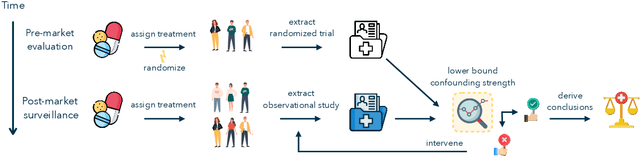
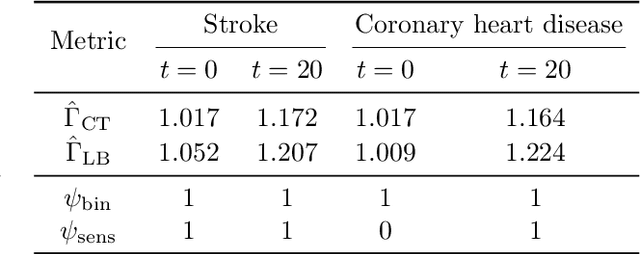
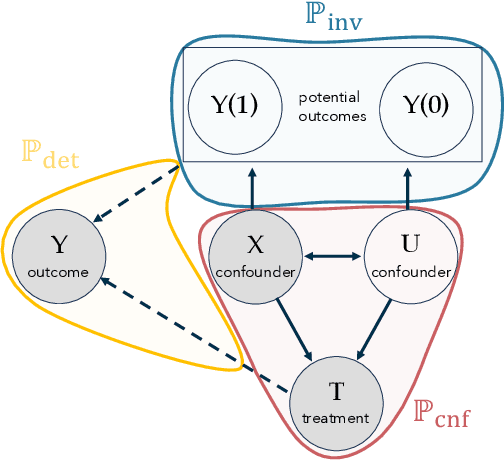
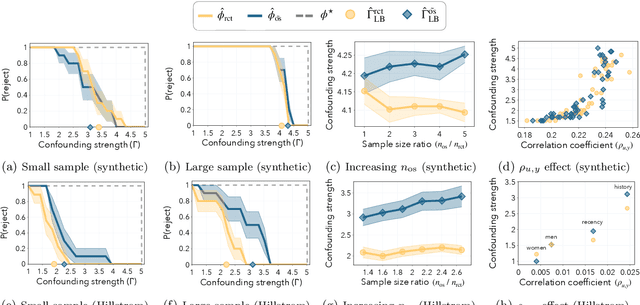
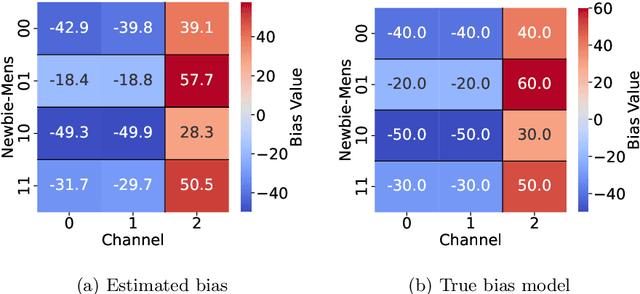
In the era of fast-paced precision medicine, observational studies play a major role in properly evaluating new treatments in clinical practice. Yet, unobserved confounding can significantly compromise causal conclusions drawn from non-randomized data. We propose a novel strategy that leverages randomized trials to quantify unobserved confounding. First, we design a statistical test to detect unobserved confounding with strength above a given threshold. Then, we use the test to estimate an asymptotically valid lower bound on the unobserved confounding strength. We evaluate the power and validity of our statistical test on several synthetic and semi-synthetic datasets. Further, we show how our lower bound can correctly identify the absence and presence of unobserved confounding in a real-world setting.

How robust accuracy suffers from certified training with convex relaxations

Adversarial attacks pose significant threats to deploying state-of-the-art classifiers in safety-critical applications. Two classes of methods have emerged to address this issue: empirical defences and certified defences. Although certified defences come with robustness guarantees, empirical defences such as adversarial training enjoy much higher popularity among practitioners. In this paper, we systematically compare the standard and robust error of these two robust training paradigms across multiple computer vision tasks. We show that in most tasks and for both $\mathscr{l}_\infty$-ball and $\mathscr{l}_2$-ball threat models, certified training with convex relaxations suffers from worse standard and robust error than adversarial training. We further explore how the error gap between certified and adversarial training depends on the threat model and the data distribution. In particular, besides the perturbation budget, we identify as important factors the shape of the perturbation set and the implicit margin of the data distribution. We support our arguments with extensive ablations on both synthetic and image datasets.

Challenging Common Assumptions in Convex Reinforcement Learning

The classic Reinforcement Learning (RL) formulation concerns the maximization of a scalar reward function. More recently, convex RL has been introduced to extend the RL formulation to all the objectives that are convex functions of the state distribution induced by a policy. Notably, convex RL covers several relevant applications that do not fall into the scalar formulation, including imitation learning, risk-averse RL, and pure exploration. In classic RL, it is common to optimize an infinite trials objective, which accounts for the state distribution instead of the empirical state visitation frequencies, even though the actual number of trajectories is always finite in practice. This is theoretically sound since the infinite trials and finite trials objectives can be proved to coincide and thus lead to the same optimal policy. In this paper, we show that this hidden assumption does not hold in the convex RL setting. In particular, we show that erroneously optimizing the infinite trials objective in place of the actual finite trials one, as it is usually done, can lead to a significant approximation error. Since the finite trials setting is the default in both simulated and real-world RL, we believe shedding light on this issue will lead to better approaches and methodologies for convex RL, impacting relevant research areas such as imitation learning, risk-averse RL, and pure exploration among others.