Subgraph Matching via Partial Optimal Transport
Paper and Code
Jun 28, 2024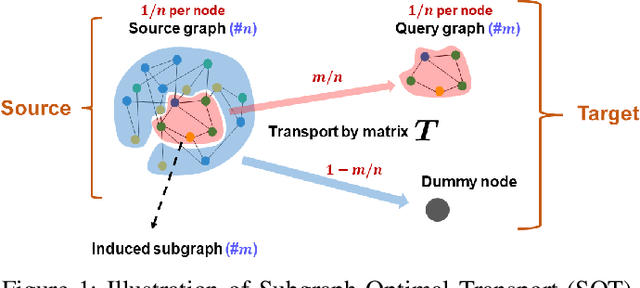
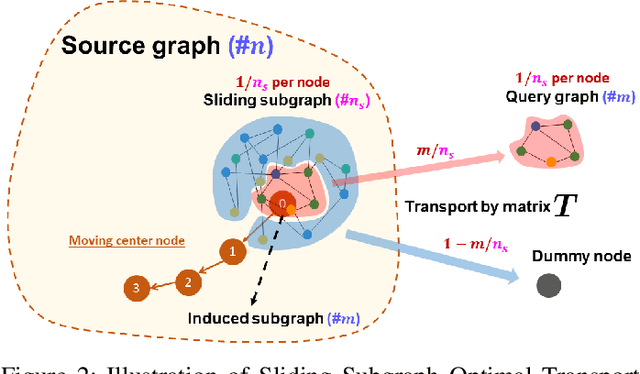
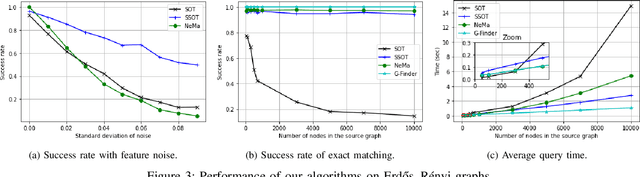
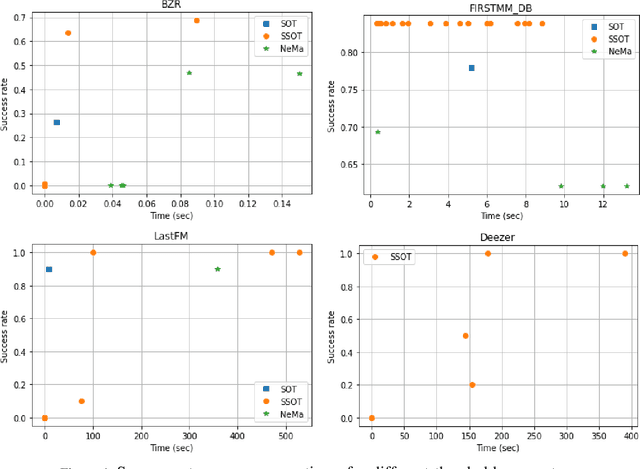
In this work, we propose a novel approach for subgraph matching, the problem of finding a given query graph in a large source graph, based on the fused Gromov-Wasserstein distance. We formulate the subgraph matching problem as a partial fused Gromov-Wasserstein problem, which allows us to build on existing theory and computational methods in order to solve this challenging problem. We extend our method by employing a subgraph sliding approach, which makes it efficient even for large graphs. In numerical experiments, we showcase that our new algorithms have the ability to outperform state-of-the-art methods for subgraph matching on synthetic as well as realworld datasets. In particular, our methods exhibit robustness with respect to noise in the datasets and achieve very fast query times.
 Add to Chrome
Add to Chrome Add to Firefox
Add to Firefox Add to Edge
Add to Edge